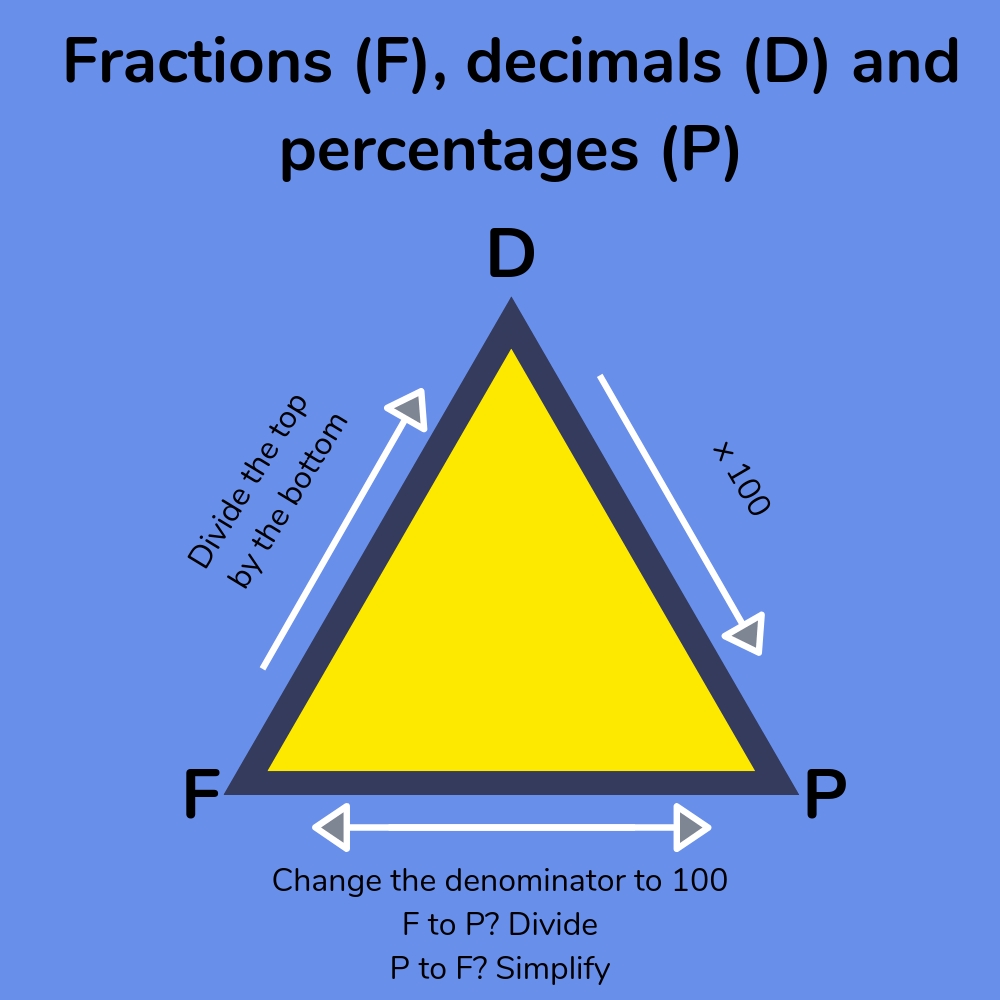
6 Ways to Compare Fractions With Unlike Denominators
Comparing Fractions with Unlike Denominators: A Comprehensive Guide
When it comes to fractions, comparing them can be a bit tricky, especially when they have unlike denominators. However, with the right strategies and techniques, you can easily compare fractions and determine which one is larger or smaller. In this article, we will explore six ways to compare fractions with unlike denominators.
Method 1: Finding the Least Common Multiple (LCM)
One way to compare fractions with unlike denominators is to find the least common multiple (LCM) of the two denominators. The LCM is the smallest number that both denominators can divide into evenly. Once you have found the LCM, you can convert both fractions to have the same denominator, making it easy to compare them.
For example, let’s compare the fractions 1⁄4 and 1⁄6. The LCM of 4 and 6 is 12. So, we can convert both fractions to have a denominator of 12:
1⁄4 = 3⁄12 1⁄6 = 2⁄12
Now we can see that 3⁄12 is greater than 2⁄12.
📝 Note: Finding the LCM can be a bit time-consuming, but it's a great way to compare fractions with unlike denominators.
Method 2: Using Equivalent Fractions
Another way to compare fractions with unlike denominators is to use equivalent fractions. Equivalent fractions are fractions that have the same value but different denominators. You can create equivalent fractions by multiplying or dividing both the numerator and denominator by the same number.
For example, let’s compare the fractions 2⁄3 and 3⁄4. We can create equivalent fractions by multiplying the numerator and denominator of the first fraction by 4, and the numerator and denominator of the second fraction by 3:
2⁄3 = 8⁄12 3⁄4 = 9⁄12
Now we can see that 9⁄12 is greater than 8⁄12.
Method 3: Cross-Multiplication
Cross-multiplication is a quick and easy way to compare fractions with unlike denominators. To cross-multiply, you multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. Then, you compare the products.
For example, let’s compare the fractions 2⁄3 and 3⁄4. We can cross-multiply as follows:
2 × 4 = 8 3 × 3 = 9
Since 9 is greater than 8, we know that 3⁄4 is greater than 2⁄3.
📝 Note: Cross-multiplication is a great way to compare fractions quickly, but it only works if the fractions are not equal.
Method 4: Using a Number Line
A number line is a visual tool that can help you compare fractions with unlike denominators. To use a number line, you plot the fractions on the line and see which one is farther to the right.
For example, let’s compare the fractions 1⁄2 and 2⁄3. We can plot these fractions on a number line as follows:
1⁄2 = 0.5 2⁄3 = 0.67
Since 0.67 is farther to the right than 0.5, we know that 2⁄3 is greater than 1⁄2.
Method 5: Converting to Decimals
Converting fractions to decimals is another way to compare fractions with unlike denominators. To convert a fraction to a decimal, you divide the numerator by the denominator.
For example, let’s compare the fractions 3⁄4 and 2⁄3. We can convert these fractions to decimals as follows:
3⁄4 = 0.75 2⁄3 = 0.67
Since 0.75 is greater than 0.67, we know that 3⁄4 is greater than 2⁄3.
Method 6: Using a Fraction Wall
A fraction wall is a visual tool that can help you compare fractions with unlike denominators. A fraction wall is a diagram that shows the relationships between different fractions.
For example, let’s compare the fractions 1⁄2 and 2⁄3. We can use a fraction wall to see which one is larger:
1⁄2 = 1⁄2 2⁄3 = 1⁄2 + 1⁄6
Since 2⁄3 is equal to 1⁄2 + 1⁄6, we know that 2⁄3 is greater than 1⁄2.
What is the easiest way to compare fractions with unlike denominators?
+The easiest way to compare fractions with unlike denominators is to use cross-multiplication. This method involves multiplying the numerator of the first fraction by the denominator of the second fraction, and vice versa. Then, you compare the products.
Can I use a number line to compare fractions with unlike denominators?
+Yes, you can use a number line to compare fractions with unlike denominators. This method involves plotting the fractions on the line and seeing which one is farther to the right.
What is the least common multiple (LCM) of two denominators?
+The least common multiple (LCM) of two denominators is the smallest number that both denominators can divide into evenly. You can use the LCM to compare fractions with unlike denominators by converting both fractions to have the same denominator.
In conclusion, comparing fractions with unlike denominators can be a bit tricky, but with the right strategies and techniques, you can easily determine which fraction is larger or smaller. By using methods such as finding the least common multiple, using equivalent fractions, cross-multiplication, number lines, converting to decimals, and fraction walls, you can compare fractions with unlike denominators with confidence.
Related Terms:
- Comparing fractions same denominator
- Comparing fractions Worksheet grade 4
- Comparing fractions Worksheet same denominator