5 Ways to Compare Fractions with Same Denominator
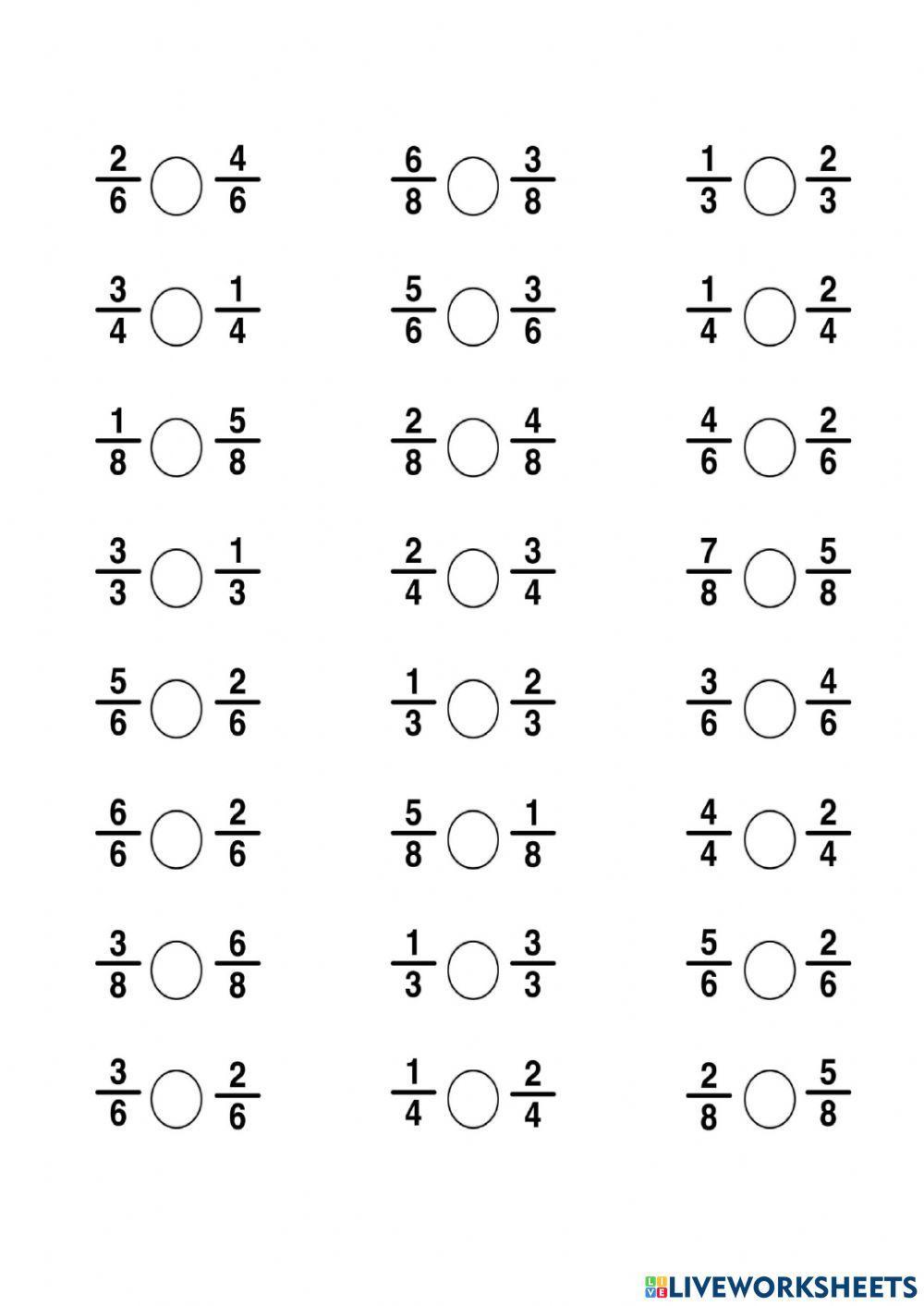
Comparing Fractions with the Same Denominator: A Step-by-Step Guide
When dealing with fractions, comparing them can be a bit tricky. However, when the denominators are the same, the process becomes much simpler. In this article, we will explore 5 ways to compare fractions with the same denominator, along with examples and explanations to help you understand the concepts better.
What are Fractions with the Same Denominator?
Fractions with the same denominator are fractions that have the same number in the denominator, but different numbers in the numerator. For example, 1⁄4 and 3⁄4 are fractions with the same denominator, which is 4.
Why Compare Fractions with the Same Denominator?
Comparing fractions with the same denominator is essential in various mathematical operations, such as addition, subtraction, multiplication, and division. It also helps in understanding the relationships between different fractions and how they can be used to solve problems.
Method 1: Comparing Fractions with the Same Denominator by Looking at the Numerators
When comparing fractions with the same denominator, the easiest way is to look at the numerators. The fraction with the larger numerator is the larger fraction.
📝 Note: This method only works when the denominators are the same.
Example:
Compare 2⁄5 and 3⁄5.
Since the denominators are the same (5), we can compare the numerators. 3 is greater than 2, so 3⁄5 is greater than 2⁄5.
Method 2: Using Visual Aids to Compare Fractions
Visual aids, such as circles or rectangles, can be used to compare fractions with the same denominator. By shading or coloring the same amount of each shape, we can easily compare the fractions.
Example:
Compare 1⁄4 and 3⁄4 using a circle.
Divide the circle into 4 equal parts and shade 1 part for 1⁄4 and 3 parts for 3⁄4. Since 3 parts are shaded for 3⁄4, it is clear that 3⁄4 is greater than 1⁄4.
Method 3: Converting Fractions to Decimals to Compare
Another way to compare fractions with the same denominator is to convert them to decimals. This method involves dividing the numerator by the denominator to get the decimal equivalent.
Example:
Compare 2⁄5 and 3⁄5 by converting them to decimals.
Divide 2 by 5 to get 0.4, and divide 3 by 5 to get 0.6. Since 0.6 is greater than 0.4, 3⁄5 is greater than 2⁄5.
Method 4: Using Real-World Examples to Compare Fractions
Real-world examples can be used to compare fractions with the same denominator. By using everyday objects or situations, we can make the comparison more meaningful and easier to understand.
Example:
Compare 1⁄4 and 3⁄4 using a pizza.
Imagine a pizza that is divided into 4 equal slices. If you eat 1 slice, you have eaten 1⁄4 of the pizza. If your friend eats 3 slices, they have eaten 3⁄4 of the pizza. Since 3 slices are more than 1 slice, 3⁄4 is greater than 1⁄4.
Method 5: Creating a Number Line to Compare Fractions
A number line can be used to compare fractions with the same denominator. By marking the fractions on the number line, we can visualize their relationships and compare them easily.
Example:
Compare 2⁄5 and 3⁄5 using a number line.
Mark the fractions 0, 1⁄5, 2⁄5, 3⁄5, and 4⁄5 on the number line. Since 3⁄5 is to the right of 2⁄5, it is clear that 3⁄5 is greater than 2⁄5.
Conclusion
Comparing fractions with the same denominator is a crucial skill in mathematics. By using the 5 methods outlined in this article, you can easily compare fractions and understand their relationships. Whether you use visual aids, convert to decimals, or create a number line, the key is to find a method that works best for you.
What is the easiest way to compare fractions with the same denominator?
+
The easiest way to compare fractions with the same denominator is to look at the numerators. The fraction with the larger numerator is the larger fraction.
Can I compare fractions with different denominators using the same methods?
+
No, the methods outlined in this article only work for fractions with the same denominator. To compare fractions with different denominators, you need to find the least common multiple (LCM) or use other methods.
How can I apply comparing fractions to real-life situations?
+
Comparing fractions can be applied to various real-life situations, such as measuring ingredients for a recipe, dividing a pizza among friends, or comparing the sizes of different objects.
Related Terms:
- Comparing fractions with same denominator
- Comparing fractions Worksheet with answers
- Comparing fractions Worksheet Grade 5
- Comparing fractions Worksheet grade 4