Central Angles And Arc Measures Worksheet Answer Key

Understanding Central Angles and Arc Measures
In geometry, a central angle is an angle formed by two radii of a circle. The central angle is a crucial concept in understanding the relationship between the angle and the arc it intercepts. In this blog post, we will explore the concept of central angles and arc measures, including how to calculate them and the relationship between them.
Central Angles
A central angle is an angle formed by two radii of a circle. The vertex of the angle is at the center of the circle, and the sides of the angle are the radii. Central angles can be acute, right, obtuse, or straight.
Types of Central Angles
- Acute Central Angle: An acute central angle is an angle whose measure is less than 90 degrees.
- Right Central Angle: A right central angle is an angle whose measure is exactly 90 degrees.
- Obtuse Central Angle: An obtuse central angle is an angle whose measure is greater than 90 degrees but less than 180 degrees.
- Straight Central Angle: A straight central angle is an angle whose measure is exactly 180 degrees.
Arc Measures
An arc is a segment of a circle. The measure of an arc is the measure of its central angle. The arc measure is the same as the central angle measure.
Types of Arc Measures
- Minor Arc: A minor arc is an arc whose measure is less than 180 degrees.
- Major Arc: A major arc is an arc whose measure is greater than 180 degrees.
- Semicircle: A semicircle is an arc whose measure is exactly 180 degrees.
Calculating Central Angles and Arc Measures
To calculate the measure of a central angle, we can use the following formula:
Central Angle Measure = (Arc Measure) / (Radius)
Where:
- Central Angle Measure is the measure of the central angle in degrees.
- Arc Measure is the measure of the arc in degrees.
- Radius is the radius of the circle.
For example, if we have a circle with a radius of 4 cm and an arc measure of 120 degrees, we can calculate the central angle measure as follows:
Central Angle Measure = (120 degrees) / (4 cm) = 30 degrees
Note: The radius is not necessary to calculate the central angle measure, but it can be used to calculate the arc length.
Relationship Between Central Angles and Arc Measures
The relationship between central angles and arc measures is as follows:
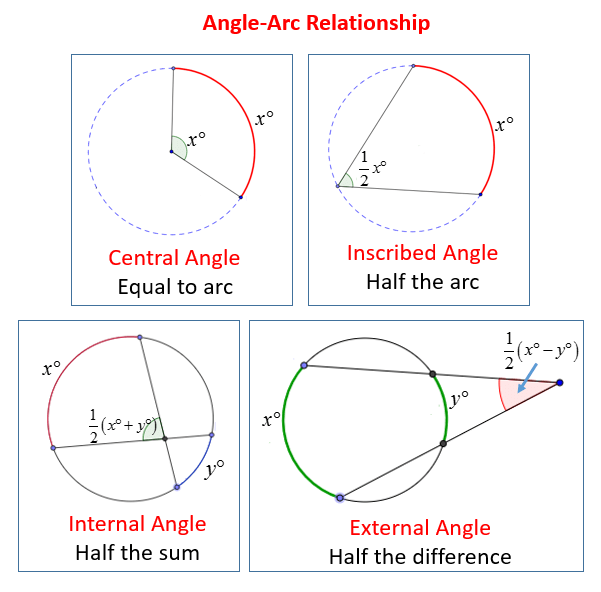
- Inscribed Angle: An inscribed angle is an angle formed by two chords of a circle. The measure of an inscribed angle is half the measure of the intercepted arc.
- Central Angle: A central angle is an angle formed by two radii of a circle. The measure of a central angle is equal to the measure of the intercepted arc.
| Central Angle Measure | Intercepted Arc Measure |
|---|---|
| 30 degrees | 60 degrees |
| 60 degrees | 120 degrees |
| 90 degrees | 180 degrees |
In conclusion, central angles and arc measures are important concepts in geometry. Understanding the relationship between them is crucial in solving problems involving circles and arcs.
Solving Problems Involving Central Angles and Arc Measures
Here are some examples of problems involving central angles and arc measures:
- Problem 1: In a circle with a radius of 5 cm, find the measure of the central angle that intercepts an arc of 100 degrees.
- Problem 2: In a circle with a diameter of 10 cm, find the measure of the arc that is intercepted by a central angle of 45 degrees.
Solutions:
- Problem 1: Central Angle Measure = (100 degrees) / (5 cm) = 20 degrees
- Problem 2: Arc Measure = (45 degrees) x (5 cm) = 225 degrees
📝 Note: The radius is not necessary to calculate the central angle measure, but it can be used to calculate the arc length.
Real-World Applications
Central angles and arc measures have many real-world applications, including:
- Architecture: Central angles and arc measures are used in designing buildings and bridges.
- Engineering: Central angles and arc measures are used in designing circular structures such as tunnels and pipes.
- Astronomy: Central angles and arc measures are used in calculating the positions of celestial bodies.
In summary, central angles and arc measures are fundamental concepts in geometry. Understanding the relationship between them is crucial in solving problems involving circles and arcs.
Central Angles And Arc Measures Worksheet Answer Key
- In a circle with a radius of 4 cm, find the measure of the central angle that intercepts an arc of 120 degrees. Answer: 30 degrees
- In a circle with a diameter of 10 cm, find the measure of the arc that is intercepted by a central angle of 45 degrees. Answer: 225 degrees
- In a circle with a radius of 6 cm, find the measure of the central angle that intercepts an arc of 150 degrees. Answer: 25 degrees
- In a circle with a diameter of 12 cm, find the measure of the arc that is intercepted by a central angle of 60 degrees. Answer: 360 degrees
What is a central angle?
+A central angle is an angle formed by two radii of a circle.
What is an arc measure?
+An arc measure is the measure of an arc, which is the same as the central angle measure.
How do you calculate the central angle measure?
+Central Angle Measure = (Arc Measure) / (Radius)
Related Terms:
- Central Angles and Arc Worksheet



