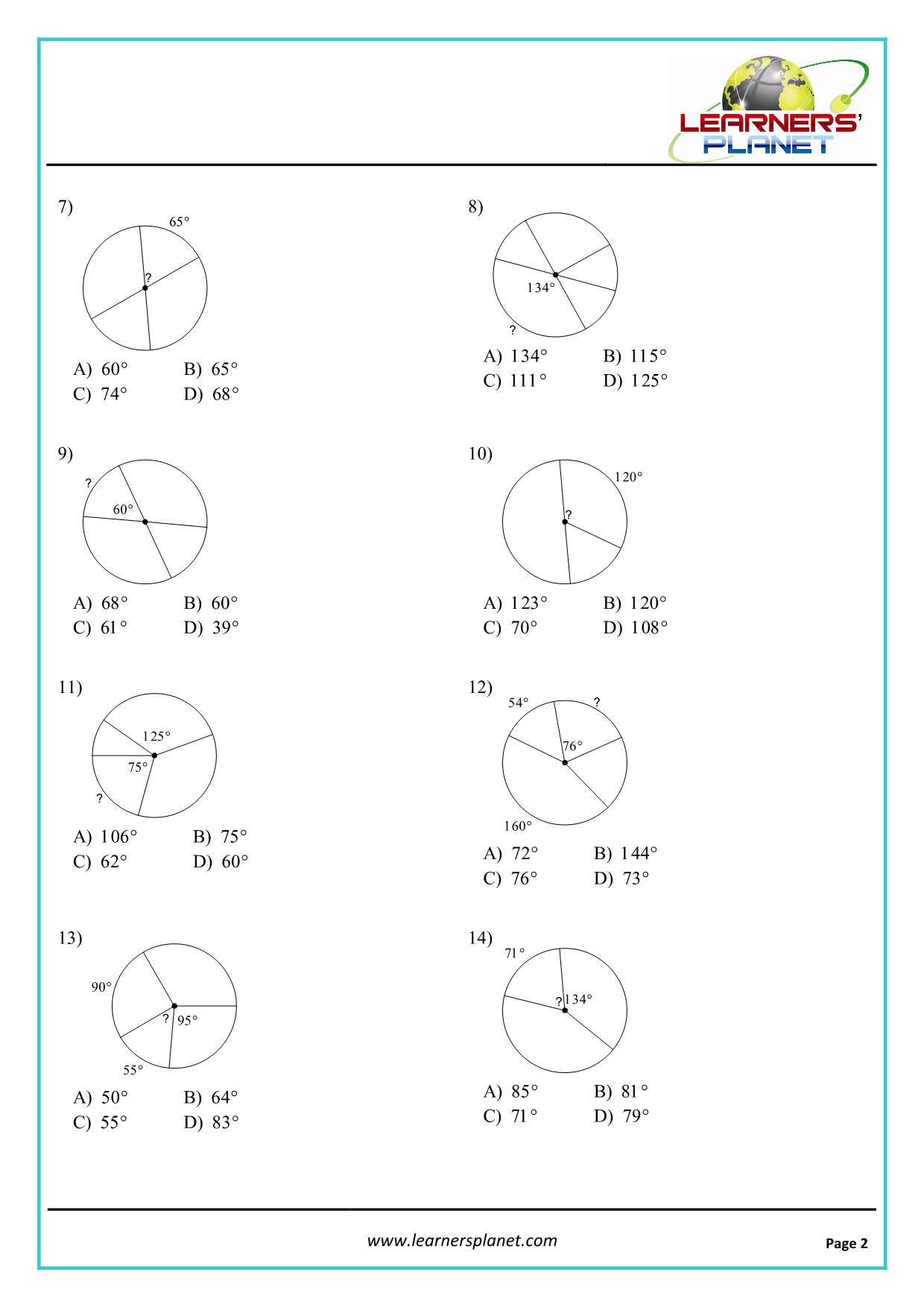
Central Angle Worksheet: Mastering Circle Geometry Made Easy
Understanding Central Angles: A Key to Unlocking Circle Geometry
Circle geometry is a fundamental concept in mathematics, and mastering it requires a deep understanding of central angles. A central angle is an angle whose vertex is at the center of a circle, and its sides pass through the endpoints of an arc. In this article, we will delve into the world of central angles, exploring their properties, formulas, and applications.
What is a Central Angle?
A central angle is an angle formed by two radii of a circle. It is called a central angle because its vertex is at the center of the circle. The sides of the central angle are the radii, and the arc intercepted by the central angle is called the intercepted arc.
📝 Note: A central angle is always a positive angle, and its measure is always less than 360 degrees.
Properties of Central Angles
Central angles have several important properties that make them useful in circle geometry. Here are some of the key properties:
- The measure of a central angle is equal to the measure of its intercepted arc: This means that if you know the measure of the central angle, you can find the measure of the intercepted arc, and vice versa.
- The sum of the measures of the central angles in a circle is 360 degrees: This property is useful when working with multiple central angles in a circle.
- Central angles are congruent if and only if their intercepted arcs are congruent: This means that if two central angles have congruent intercepted arcs, then the central angles are congruent.
Formulas for Central Angles
Here are some important formulas related to central angles:
- Central Angle Formula: The measure of a central angle (in degrees) is equal to the ratio of the length of the intercepted arc to the circumference of the circle.
- Arc Length Formula: The length of an arc is equal to the circumference of the circle multiplied by the ratio of the measure of the central angle to 360 degrees.
| Formula | Description |
|---|---|
| Central Angle Formula | m∠AOB = (length of arc AB / circumference of circle) × 360° |
| Arc Length Formula | length of arc AB = (circumference of circle) × (m∠AOB / 360°) |
Applications of Central Angles
Central angles have numerous applications in real-world problems, including:
- Geometry: Central angles are used to find the measures of arcs and angles in circles.
- Trigonometry: Central angles are used to define the trigonometric functions, such as sine, cosine, and tangent.
- Physics: Central angles are used to describe the motion of objects in circular paths.
Central Angle Worksheet: Practice Problems
Here are some practice problems to help you master central angles:
- Find the measure of the central angle if the length of the intercepted arc is 30 cm and the circumference of the circle is 120 cm.
- Find the length of the intercepted arc if the measure of the central angle is 60° and the circumference of the circle is 240 cm.
- Find the measure of the central angle if the intercepted arc subtends an angle of 120° at the center of the circle.
Solving Central Angle Problems
To solve central angle problems, follow these steps:
- Read the problem carefully and identify the given information.
- Draw a diagram to visualize the problem.
- Use the formulas and properties of central angles to solve the problem.
📝 Note: Always check your units when working with central angles. Make sure you are using the correct units for the length of the arc and the circumference of the circle.
By mastering central angles, you will be able to solve a wide range of problems in circle geometry. Remember to practice regularly and apply the formulas and properties of central angles to different types of problems.
In summary, central angles are a fundamental concept in circle geometry, and understanding their properties and formulas is essential for solving problems in this area. With practice and patience, you can become proficient in working with central angles and unlock the secrets of circle geometry.
What is the difference between a central angle and an inscribed angle?
+A central angle is an angle whose vertex is at the center of a circle, while an inscribed angle is an angle whose vertex is on the circle. The central angle intercepts an arc, while the inscribed angle subtends an arc.
How do you find the measure of a central angle if you know the length of the intercepted arc?
+You can use the central angle formula: m∠AOB = (length of arc AB / circumference of circle) × 360°
What is the sum of the measures of the central angles in a circle?
+The sum of the measures of the central angles in a circle is 360 degrees.
Related Terms:
- Inscribed angle worksheet



