Area of Parallelograms Worksheet and Solutions

Understanding the Concept of Parallelograms and Their Areas

Parallelograms are a type of quadrilateral where the opposite sides are parallel to each other. They are an essential concept in geometry, and understanding their properties is crucial for solving problems related to perimeter, area, and volume. In this article, we will delve into the concept of parallelograms, their characteristics, and most importantly, how to calculate their area.

Properties of Parallelograms

Before we dive into the area calculation, let’s first understand the properties of parallelograms. Some of the key properties include:

• Opposite sides are equal in length and parallel to each other.
• Opposite angles are equal.
• The area of a parallelogram is equal to the product of its base and height.
• The perimeter of a parallelogram is the sum of the lengths of all its sides.

Calculating the Area of a Parallelogram

The formula to calculate the area of a parallelogram is:

Area = Base × Height

The base of a parallelogram is any side of the shape, and the height is the perpendicular distance from the base to the opposite side.

For example, if the base of a parallelogram is 5 cm and the height is 3 cm, the area would be:

Area = 5 cm × 3 cm = 15 cm²

Derivation of the Formula

The formula for the area of a parallelogram can be derived by considering a rectangle with the same base and height as the parallelogram.

Imagine a rectangle with a base of 5 cm and a height of 3 cm. The area of this rectangle would be:

Area = Base × Height = 5 cm × 3 cm = 15 cm²

Now, if we were to cut this rectangle into two equal parts and slide one part over the other, we would form a parallelogram. The area of this parallelogram would still be 15 cm², as the base and height remain the same.

Solving Problems with Parallelograms

Let’s consider a few examples to solidify our understanding of calculating the area of parallelograms.

Example 1: Find the area of a parallelogram with a base of 6 cm and a height of 4 cm.

Solution: Using the formula, we get:

Area = Base × Height = 6 cm × 4 cm = 24 cm²

Example 2: Find the area of a parallelogram with a base of 8 cm and a height of 5 cm.

Solution: Using the formula, we get:

Area = Base × Height = 8 cm × 5 cm = 40 cm²

Common Mistakes to Avoid

When calculating the area of a parallelogram, it’s essential to avoid common mistakes that can lead to incorrect answers. Here are a few things to watch out for:

• Incorrect base or height: Make sure to identify the correct base and height of the parallelogram before plugging in the values.
• Units mismatch: Ensure that the units of measurement for the base and height are the same.
• Calculation errors: Double-check your calculations to avoid simple arithmetic mistakes.

🤔 Note: Always verify the units of measurement and calculation to ensure accuracy.

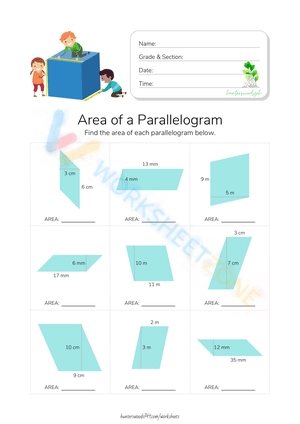
Area of Parallelograms Worksheet

Now that we’ve covered the concept of parallelograms and how to calculate their area, let’s put our skills to the test with a worksheet!

Worksheet:

Find the area of each parallelogram:

1. Base: 4 cm, Height: 6 cm
2. Base: 9 cm, Height: 3 cm
3. Base: 7 cm, Height: 5 cm
4. Base: 10 cm, Height: 2 cm
5. Base: 6 cm, Height: 8 cm

Solutions:

1. Area = 4 cm × 6 cm = 24 cm²
2. Area = 9 cm × 3 cm = 27 cm²
3. Area = 7 cm × 5 cm = 35 cm²
4. Area = 10 cm × 2 cm = 20 cm²
5. Area = 6 cm × 8 cm = 48 cm²

The area of a parallelogram is a fundamental concept in geometry, and mastering it can help you solve a variety of problems. Remember to always identify the correct base and height, verify the units of measurement, and double-check your calculations to ensure accuracy.

The concept of parallelograms and their areas is a building block for more advanced geometric concepts. With practice and patience, you can become proficient in solving problems related to parallelograms and other geometric shapes.