Area of Irregular Shapes Worksheet Solutions
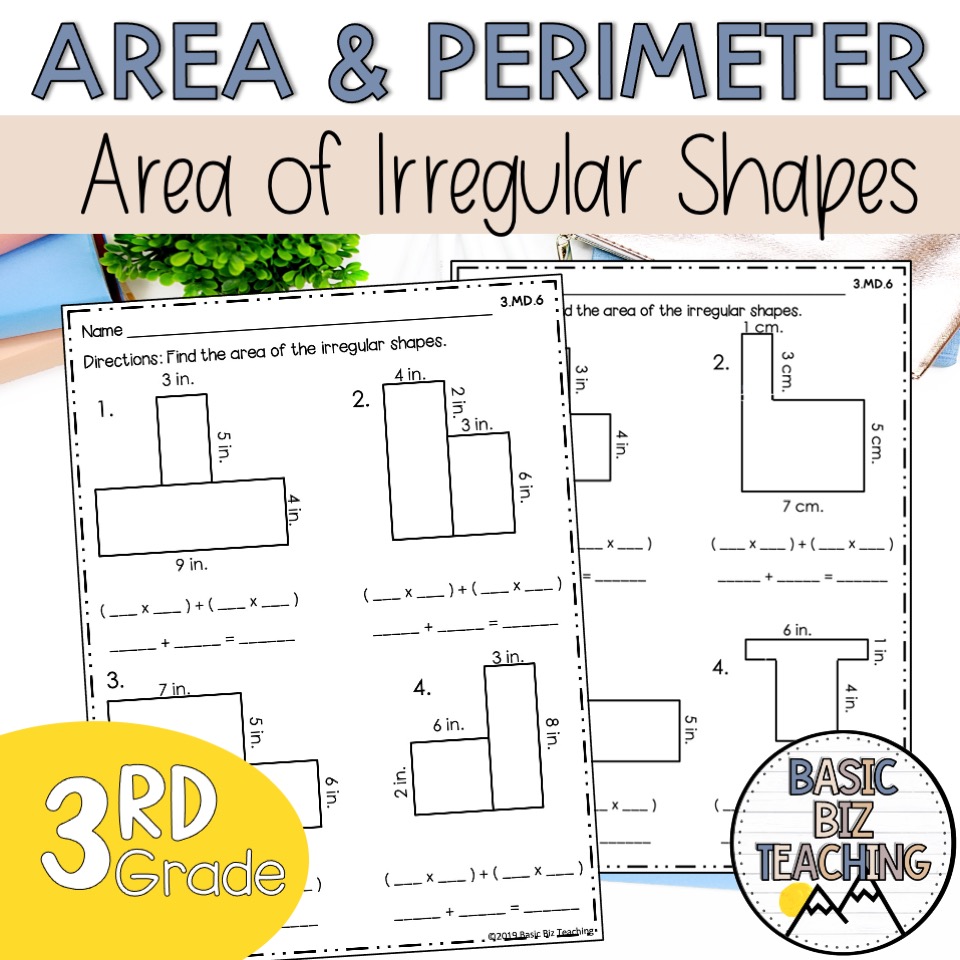
Determining the area of irregular shapes is an essential skill in mathematics, particularly in geometry. An irregular shape is a polygon that does not have equal sides or equal angles. Finding the area of such shapes requires breaking them down into simpler shapes whose area can be easily calculated. This approach simplifies the process and makes it manageable.
Understanding Irregular Shapes
Irregular shapes can be divided into two main categories: - Plane Irregular Shapes: These are two-dimensional shapes with no equal sides or angles. Examples include irregular quadrilaterals, polygons, and irregular triangles. - Solid Irregular Shapes: These are three-dimensional shapes with no equal sides or angles. Examples include irregular prisms, pyramids, and polyhedra.
Calculating Area of Irregular Shapes
The area of irregular shapes can be calculated by breaking down the shape into simpler regular shapes such as triangles, squares, and rectangles, and then summing the areas of these simpler shapes.
Method 1: Divide into Simple Shapes
📝 Note: This method is suitable for plane irregular shapes.
- Identify the Shape: First, identify the type of irregular shape you are dealing with. This could be an irregular polygon, a shape with curves, or a combination of different shapes.
- Divide into Simpler Shapes: Break down the irregular shape into simpler shapes whose area can be easily calculated. For example, an irregular quadrilateral can be divided into two triangles.
- Calculate Area of Each Shape: Calculate the area of each simpler shape using the appropriate formula. For example, the area of a triangle is given by the formula: A = ½ × base × height.
- Sum the Areas: Finally, sum the areas of the simpler shapes to get the total area of the irregular shape.
Example: Calculate the Area of an Irregular Quadrilateral
| Shape | Base | Height | Area Formula | Area |
|---|---|---|---|---|
| Triangle 1 | 5 cm | 6 cm | A = ½ × b × h | A = ½ × 5 × 6 = 15 cm² |
| Triangle 2 | 4 cm | 8 cm | A = ½ × b × h | A = ½ × 4 × 8 = 16 cm² |
Total Area = Area of Triangle 1 + Area of Triangle 2 = 15 cm² + 16 cm² = 31 cm²
Method 2: Use of Coordinate Geometry
📝 Note: This method is particularly useful for irregular polygons.
- Plot Points: Plot the vertices of the irregular polygon on a coordinate plane.
- Apply the Shoelace Formula: Use the shoelace formula to calculate the area of the polygon. The shoelace formula is given by: A = ½ |(x1y2 + x2y3 +… + xn-1yn + xny1) - (y1x2 + y2x3 +… + yn-1xn + ynx1)|
Example: Calculate the Area of an Irregular Pentagon
| Point | x-coordinate | y-coordinate |
|---|---|---|
| A | 1 | 2 |
| B | 3 | 4 |
| C | 5 | 1 |
| D | 2 | 3 |
| E | 1 | 1 |
Apply the shoelace formula to calculate the area.
Solutions to Common Problems
| Shape | Solution |
|---|---|
| Irregular Triangle | Divide into two right-angled triangles and calculate the area of each triangle separately. |
| Irregular Quadrilateral | Divide into two triangles or a rectangle and a triangle, and sum their areas. |
| Irregular Pentagon | Use the shoelace formula or divide into three triangles and sum their areas. |
In conclusion, calculating the area of irregular shapes requires creativity in breaking down the shape into simpler, manageable parts. Whether it’s dividing into triangles, rectangles, or applying the shoelace formula, the key is to find a method that simplifies the problem, making it easier to solve.
What is the shoelace formula used for?
+The shoelace formula is used to calculate the area of a simple polygon whose vertices are described by their Cartesian coordinates in the plane.
How do I calculate the area of an irregular hexagon?
+You can calculate the area of an irregular hexagon by dividing it into four triangles and summing their areas. Alternatively, you can use the shoelace formula if you know the coordinates of the vertices.
Can I use the shoelace formula for a shape with curved sides?
+No, the shoelace formula is applicable only to simple polygons with straight sides. For shapes with curved sides, you would need to approximate the area using different methods, such as dividing the shape into smaller sections that can be approximated by polygons.



