5 Ways to Master Arc Length and Sector Area
Mastering Arc Length and Sector Area: A Comprehensive Guide
Understanding arc length and sector area is a fundamental aspect of mathematics, particularly in geometry and trigonometry. These concepts are used to calculate the length of an arc of a circle and the area of a sector, respectively. In this article, we will explore five ways to master arc length and sector area, making it easier for you to tackle problems with confidence.
1. Understanding the Basics
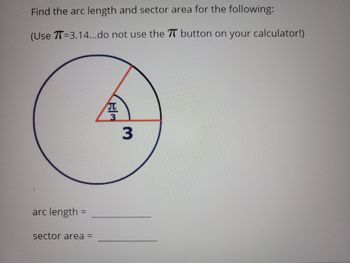
Before diving into the calculations, it’s essential to understand the basics of arc length and sector area. An arc is a segment of a circle, and its length can be calculated using the formula:
Arc Length = (θ/360) × 2πr
where θ is the central angle in degrees, and r is the radius of the circle.
A sector, on the other hand, is a region of a circle bounded by two radii and an arc. The area of a sector can be calculated using the formula:
Sector Area = (θ/360) × πr^2
2. Using the Formulae
Now that you understand the basics, it’s time to apply the formulae to calculate arc length and sector area. Here are some examples:
- Calculate the arc length of a circle with a radius of 4 cm and a central angle of 60 degrees:
- Arc Length = (60⁄360) × 2π(4) = 4π/3 cm
- Calculate the area of a sector with a radius of 6 cm and a central angle of 120 degrees:
- Sector Area = (120⁄360) × π(6)^2 = 12π cm^2
3. Applying Trigonometric Ratios
Trigonometric ratios can be used to calculate arc length and sector area when the central angle is given in radians. The formulae for arc length and sector area using trigonometric ratios are:
Arc Length = r × θ (in radians)
Sector Area = (1⁄2) × r^2 × θ (in radians)
For example, calculate the arc length of a circle with a radius of 5 cm and a central angle of π/4 radians:
- Arc Length = 5 × π/4 = 5π/4 cm
4. Visualizing the Problem
Visualizing the problem can help you better understand the relationship between the arc length and sector area. Here’s an example:
- A pizza has a diameter of 14 inches and is cut into 8 slices. What is the length of the arc of each slice?
- Draw a diagram of the pizza and label the radius, central angle, and arc length.
- Calculate the arc length using the formula: Arc Length = (θ/360) × 2πr
5. Practice, Practice, Practice
The key to mastering arc length and sector area is to practice, practice, practice. Try solving different types of problems, such as:
- Find the arc length of a circle with a radius of 3 cm and a central angle of 45 degrees.
- Calculate the area of a sector with a radius of 8 cm and a central angle of 90 degrees.
- A circular table has a diameter of 10 feet. If it is divided into 12 equal parts, what is the length of the arc of each part?
By following these five ways to master arc length and sector area, you’ll become more confident in solving problems related to these concepts.
Some important notes to keep in mind:
📝 Note: When calculating arc length and sector area, make sure to use the correct units and to label your diagrams clearly.
📝 Note: Trigonometric ratios can be used to calculate arc length and sector area when the central angle is given in radians.
To summarize, mastering arc length and sector area requires a deep understanding of the basics, the ability to apply the formulae, and practice solving different types of problems. By following these steps and visualizing the problem, you’ll become proficient in calculating arc length and sector area in no time.
What is the difference between arc length and sector area?
+Arc length refers to the length of a segment of a circle, while sector area refers to the area of a region of a circle bounded by two radii and an arc.
How do I calculate arc length and sector area when the central angle is given in radians?
+Use the formulae: Arc Length = r × θ (in radians) and Sector Area = (1⁄2) × r^2 × θ (in radians)
What are some common mistakes to avoid when calculating arc length and sector area?
+Make sure to use the correct units and label your diagrams clearly. Also, double-check your calculations and ensure that you are using the correct formulae.