6 Essential Rules for Significant Figures

Understanding Significant Figures: A Comprehensive Guide
In the realm of scientific measurements, significant figures play a crucial role in conveying the precision and accuracy of data. These figures are essential in ensuring that calculations and measurements are reliable, and any errors or uncertainties are minimized. In this article, we will delve into the six essential rules for significant figures, providing you with a comprehensive understanding of this critical concept.
Rule 1: Non-Zero Digits
The first rule states that all non-zero digits in a measurement are considered significant. This means that any digit that is not zero is significant and contributes to the overall precision of the measurement. For example, in the measurement 456.7 g, all digits (4, 5, 6, and 7) are significant.
Rule 2: Zeros Between Non-Zero Digits
The second rule states that zeros that appear between non-zero digits are also significant. These zeros serve as placeholders and indicate the precision of the measurement. For instance, in the measurement 405.08 g, the zero between the 4 and 5 is significant.
Rule 3: Leading Zeros
The third rule states that leading zeros in a measurement are not significant. These zeros only serve to indicate the magnitude of the measurement and do not contribute to its precision. For example, in the measurement 0.0456 g, the leading zeros are not significant.
Rule 4: Trailing Zeros
The fourth rule states that trailing zeros in a measurement are significant only if the measurement contains a decimal point. If the measurement does not contain a decimal point, trailing zeros are not significant. For instance, in the measurement 45.600 g, the trailing zeros are significant, whereas in the measurement 4560 g, the trailing zeros are not significant.
Rule 5: Rounding Significant Figures
The fifth rule states that when rounding significant figures, you should look at the digit to the right of the last significant figure. If this digit is less than 5, you round down, and if it is 5 or greater, you round up. For example, if you need to round 45.67 g to three significant figures, you would round up to 45.7 g.
Rule 6: Operations with Significant Figures
The sixth and final rule states that when performing mathematical operations with significant figures, the answer should have the same number of significant figures as the measurement with the fewest significant figures. For instance, if you multiply 45.67 g (four significant figures) by 2.1 g (two significant figures), the answer should have two significant figures: 95 g.
📝 Note: When performing mathematical operations, it's essential to consider the number of significant figures in each measurement to ensure accurate and reliable results.
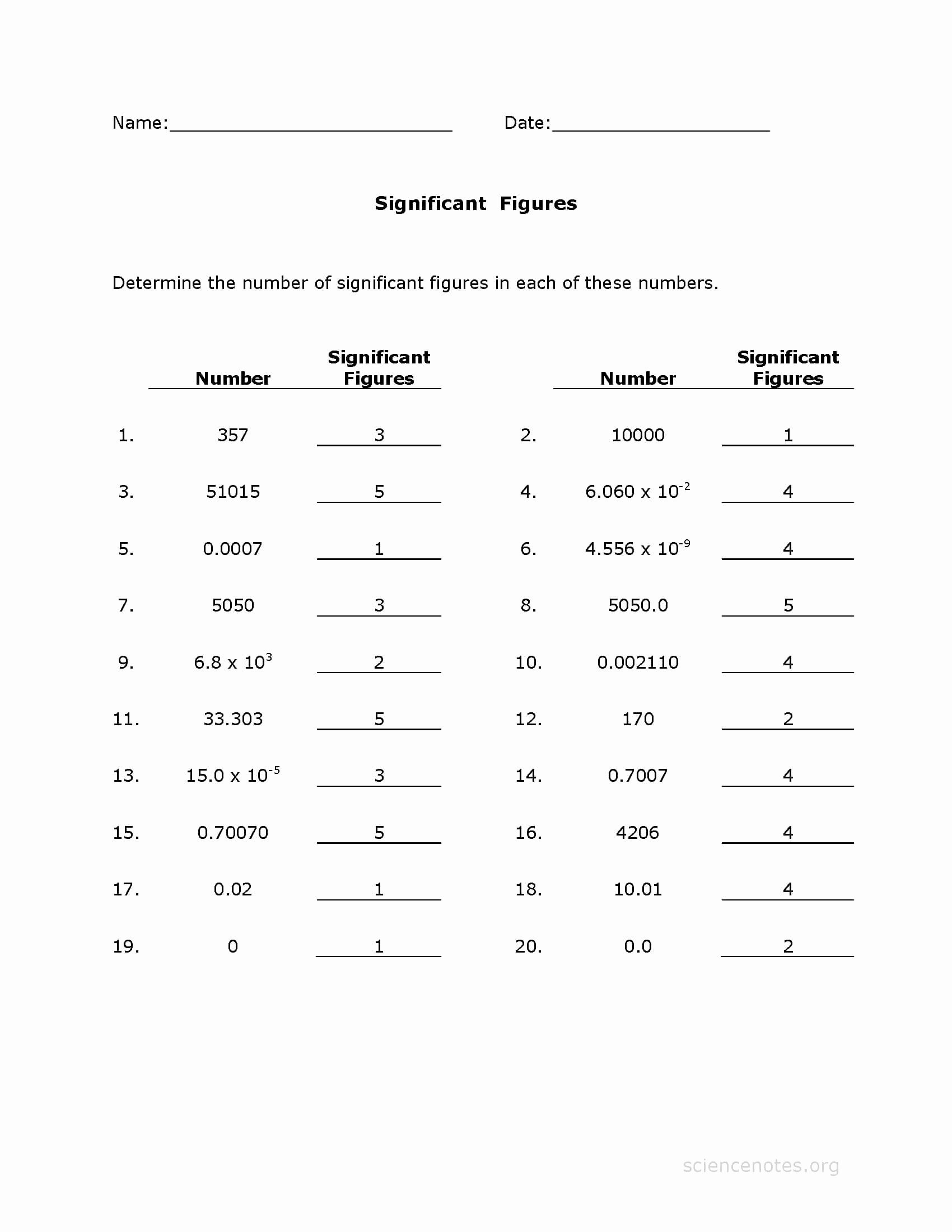
| Rule | Description | Example |
|---|---|---|
| 1. Non-Zero Digits | All non-zero digits are significant | 456.7 g (all digits are significant) |
| 2. Zeros Between Non-Zero Digits | Zeros between non-zero digits are significant | 405.08 g (zero between 4 and 5 is significant) |
| 3. Leading Zeros | Leading zeros are not significant | 0.0456 g (leading zeros are not significant) |
| 4. Trailing Zeros | Trailing zeros are significant only if there is a decimal point | 45.600 g (trailing zeros are significant) |
| 5. Rounding Significant Figures | Round up or down based on the digit to the right of the last significant figure | 45.67 g → 45.7 g (rounded to three significant figures) |
| 6. Operations with Significant Figures | The answer should have the same number of significant figures as the measurement with the fewest significant figures | 45.67 g × 2.1 g = 95 g (two significant figures) |
In conclusion, understanding significant figures is crucial in scientific measurements, and following these six essential rules ensures that your calculations and measurements are accurate and reliable. By applying these rules, you can confidently convey the precision and accuracy of your data, which is essential in various scientific fields.
What is the purpose of significant figures in scientific measurements?
+Significant figures indicate the precision and accuracy of a measurement, allowing scientists to convey the reliability of their data.
How do I determine the number of significant figures in a measurement?
+Apply the six essential rules: non-zero digits, zeros between non-zero digits, leading zeros, trailing zeros, rounding significant figures, and operations with significant figures.
Why is it important to follow the rules for significant figures in mathematical operations?
+Following the rules ensures that the answer has the correct number of significant figures, maintaining the accuracy and reliability of the calculation.
Related Terms:
- Significant figures exercises With answers
- 107.854 significant figures
- Significant figures Corbettmaths answers