7 Ways to Master Angles Formed by a Transversal
Mastering angles formed by a transversal is a crucial skill in geometry, and it’s essential to understand the different types of angles that are created when a transversal intersects two or more lines. In this article, we’ll explore 7 ways to master angles formed by a transversal, and provide you with a comprehensive guide to help you become proficient in this area.
Understanding Angles Formed by a Transversal
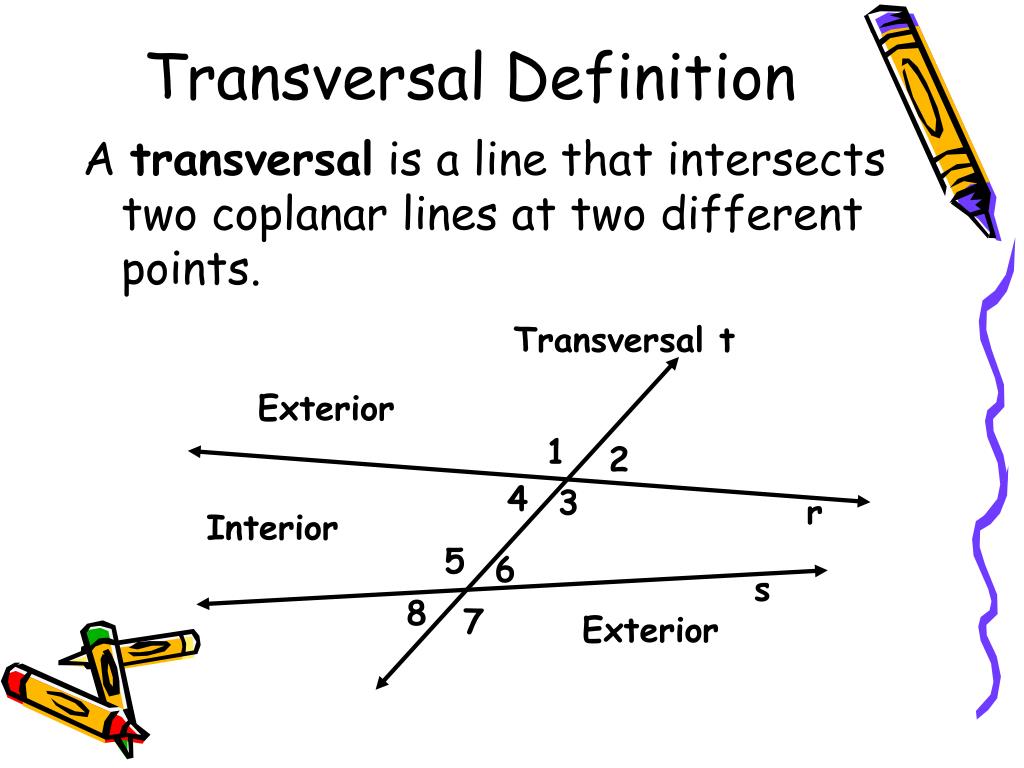
Before we dive into the 7 ways to master angles formed by a transversal, let’s take a step back and review the basics. When a transversal intersects two or more lines, it creates several types of angles, including:
- Corresponding angles
- Alternate interior angles
- Alternate exterior angles
- Interior angles on the same side of the transversal
- Exterior angles on the same side of the transversal
These angles have specific properties and relationships that are essential to understand in order to master angles formed by a transversal.
1. Identify Corresponding Angles
Corresponding angles are angles that are in the same relative position in each intersection. When a transversal intersects two lines, the corresponding angles are equal in measure. To identify corresponding angles, look for angles that are in the same position in each intersection.
- Example: In the diagram below, angles 1 and 5 are corresponding angles.

Angle 1 Angle 5 

📝 Note: Corresponding angles are equal in measure, but they are not necessarily congruent.
2. Identify Alternate Interior Angles
Alternate interior angles are angles that are on opposite sides of the transversal and inside the two lines. When a transversal intersects two lines, the alternate interior angles are equal in measure. To identify alternate interior angles, look for angles that are on opposite sides of the transversal and inside the two lines.
- Example: In the diagram below, angles 2 and 6 are alternate interior angles.
Angle 2 Angle 6 

📝 Note: Alternate interior angles are equal in measure, but they are not necessarily congruent.
3. Identify Alternate Exterior Angles
Alternate exterior angles are angles that are on opposite sides of the transversal and outside the two lines. When a transversal intersects two lines, the alternate exterior angles are equal in measure. To identify alternate exterior angles, look for angles that are on opposite sides of the transversal and outside the two lines.
- Example: In the diagram below, angles 3 and 7 are alternate exterior angles.
Angle 3 Angle 7 

📝 Note: Alternate exterior angles are equal in measure, but they are not necessarily congruent.
4. Identify Interior Angles on the Same Side of the Transversal
Interior angles on the same side of the transversal are angles that are inside the two lines and on the same side of the transversal. When a transversal intersects two lines, the interior angles on the same side of the transversal are supplementary.
- Example: In the diagram below, angles 2 and 4 are interior angles on the same side of the transversal.
Angle 2 Angle 4 

📝 Note: Interior angles on the same side of the transversal are supplementary, but they are not necessarily congruent.
5. Identify Exterior Angles on the Same Side of the Transversal
Exterior angles on the same side of the transversal are angles that are outside the two lines and on the same side of the transversal. When a transversal intersects two lines, the exterior angles on the same side of the transversal are supplementary.
- Example: In the diagram below, angles 1 and 3 are exterior angles on the same side of the transversal.
Angle 1 Angle 3 

📝 Note: Exterior angles on the same side of the transversal are supplementary, but they are not necessarily congruent.
6. Use the Transversal Theorem
The Transversal Theorem states that if two lines are cut by a transversal, then the corresponding angles are equal, the alternate interior angles are equal, and the alternate exterior angles are equal.
- Example: In the diagram below, angles 1 and 5 are corresponding angles, angles 2 and 6 are alternate interior angles, and angles 3 and 7 are alternate exterior angles.
Angle 1 Angle 5 Angle 2 Angle 6 Angle 3 Angle 7 





📝 Note: The Transversal Theorem is a powerful tool for solving problems involving angles formed by a transversal.
7. Practice, Practice, Practice
The key to mastering angles formed by a transversal is to practice, practice, practice. Try solving different types of problems, and use the strategies outlined above to help you.
In conclusion, mastering angles formed by a transversal requires a deep understanding of the different types of angles that are created when a transversal intersects two or more lines. By following the 7 strategies outlined above, you can become proficient in this area and improve your problem-solving skills.
What is a transversal?
+A transversal is a line that intersects two or more other lines.
What are corresponding angles?
+Corresponding angles are angles that are in the same relative position in each intersection.
What is the Transversal Theorem?
+The Transversal Theorem states that if two lines are cut by a transversal, then the corresponding angles are equal, the alternate interior angles are equal, and the alternate exterior angles are equal.