Angle Addition Postulate Practice Made Easy

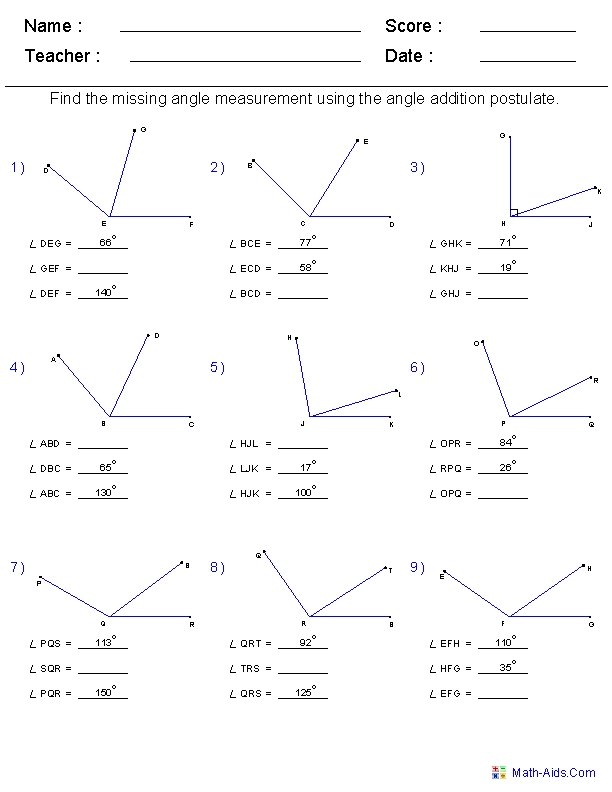
Understanding the Angle Addition Postulate

The Angle Addition Postulate is a fundamental concept in geometry that helps us find the measure of an angle by adding the measures of two adjacent angles. In this post, we will delve into the world of angle addition, explore its definition, and provide practice exercises to help you master this concept.

Definition of the Angle Addition Postulate

The Angle Addition Postulate states that if two angles, ∠A and ∠B, share a common vertex and form a straight line, then the measure of the sum of these two angles is equal to the measure of the angle formed by the straight line. Mathematically, this can be represented as:

m∠A + m∠B = m∠(A+B)

where m∠A, m∠B, and m∠(A+B) are the measures of angles A, B, and A+B, respectively.

Key Concepts to Remember

To apply the Angle Addition Postulate correctly, keep the following key concepts in mind:

• Adjacent angles: Angles that share a common vertex and a common side.
• Straight line: A line that forms a 180° angle.
• Measure of an angle: The number of degrees in an angle.

Practice Exercises

Now that we have a solid understanding of the Angle Addition Postulate, let’s put our knowledge into practice with some exercises.

Exercise 1

Find the measure of ∠A + ∠B if ∠A measures 30° and ∠B measures 60°.

Solution

m∠A + m∠B = m∠(A+B) 30° + 60° = m∠(A+B) 90° = m∠(A+B)

Exercise 2

Find the measure of ∠C if ∠A measures 45°, ∠B measures 90°, and ∠C is formed by the straight line that contains ∠A and ∠B.

Solution

m∠A + m∠B = m∠C 45° + 90° = m∠C 135° = m∠C

Exercise 3

Find the measure of ∠D if ∠A measures 120°, ∠B measures 30°, and ∠D is formed by the straight line that contains ∠A and ∠B.

Solution

m∠A + m∠B = m∠D 120° + 30° = m∠D 150° = m∠D

🤔 Note: Remember to always check if the angles form a straight line before applying the Angle Addition Postulate.

Real-World Applications

The Angle Addition Postulate has numerous real-world applications, including:

• Architecture: Designing buildings and bridges requires precise calculations of angles to ensure stability and structural integrity.
• Engineering: Engineers use angle addition to calculate stresses and loads on structures, such as bridges and buildings.
• Navigation: Pilots and sailors use angle addition to calculate courses and navigate through uncharted territories.

Common Mistakes to Avoid

When applying the Angle Addition Postulate, be mindful of the following common mistakes:

• Forgetting to check if the angles form a straight line: Ensure that the angles share a common vertex and form a straight line before applying the postulate.
• Misidentifying adjacent angles: Double-check that the angles share a common side and vertex.

By mastering the Angle Addition Postulate and avoiding common mistakes, you’ll become proficient in solving angle-related problems and develop a solid foundation in geometry.

In conclusion, the Angle Addition Postulate is a fundamental concept in geometry that helps us find the measure of an angle by adding the measures of two adjacent angles. By mastering this concept and avoiding common mistakes, you’ll become proficient in solving angle-related problems and develop a solid foundation in geometry.