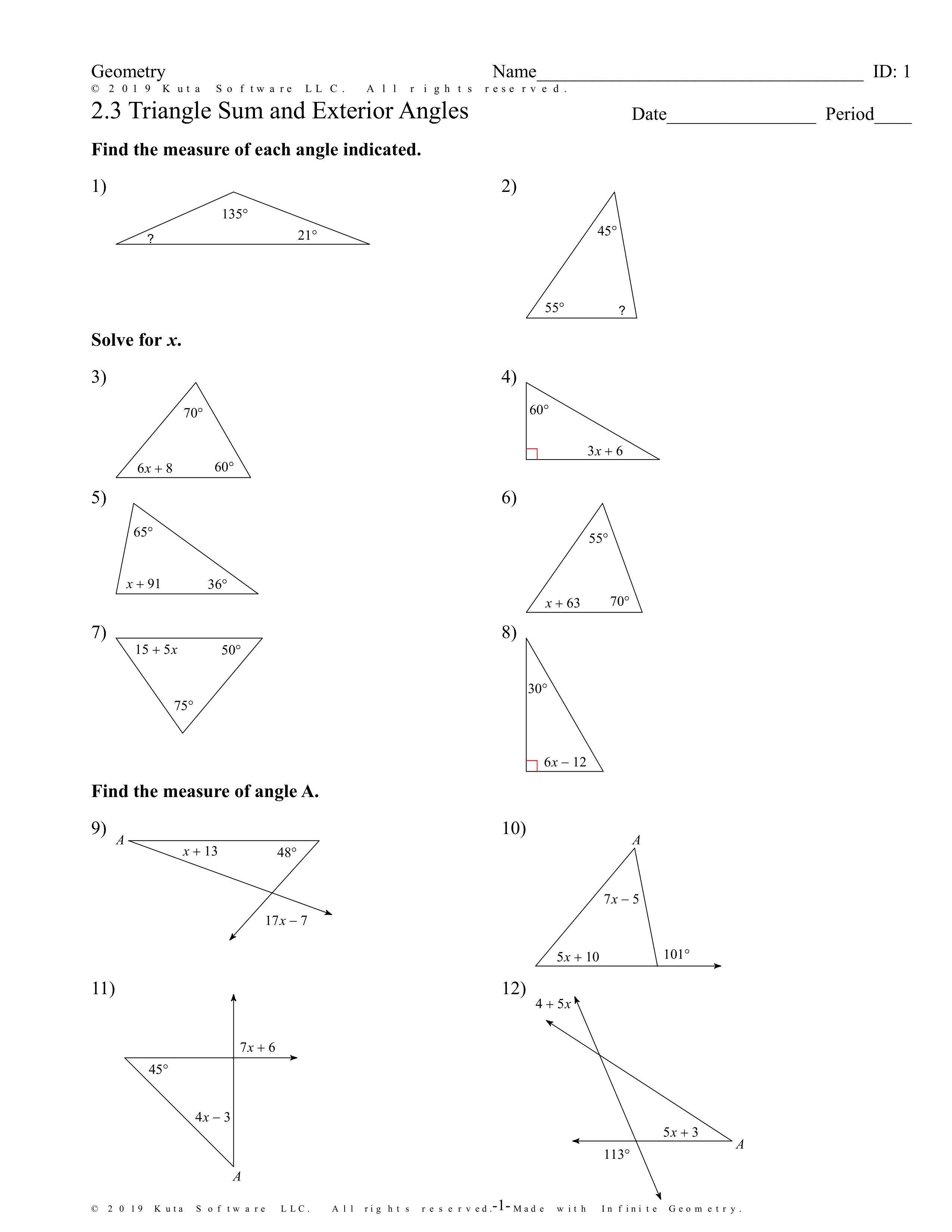
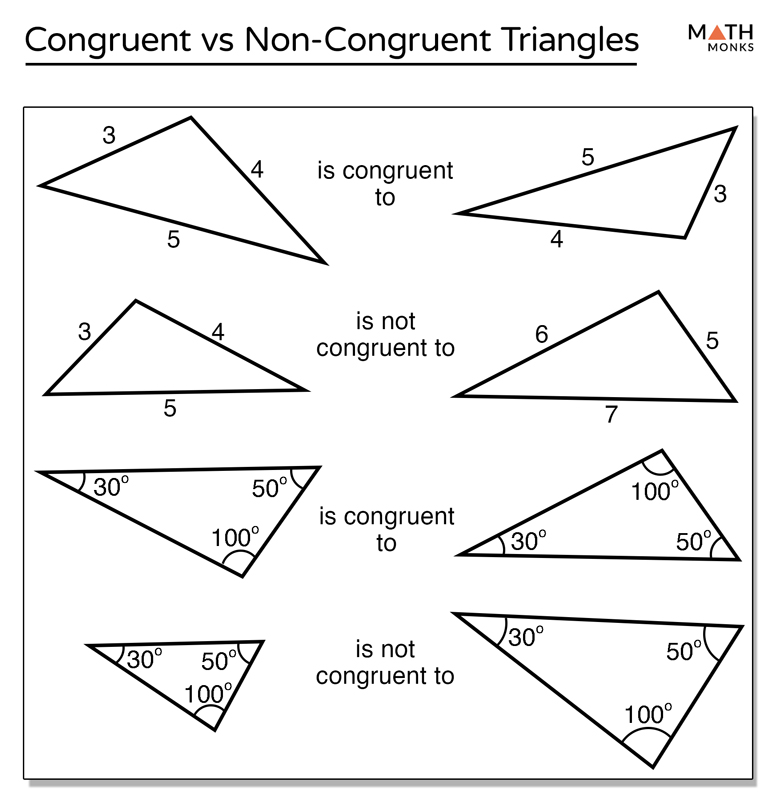
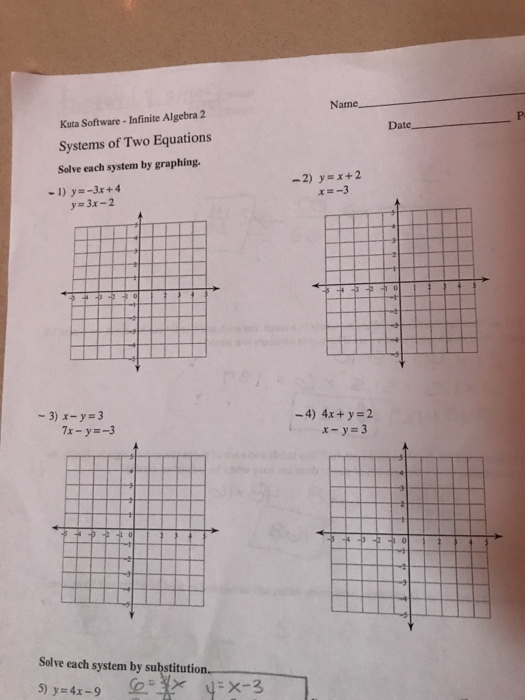
Algebra 1b Systems of Linear Inequalities Worksheet Answers

Systems of Linear Inequalities: Understanding the Basics
Systems of linear inequalities are a fundamental concept in algebra, and they have numerous applications in various fields, including economics, physics, and engineering. In this blog post, we will delve into the world of systems of linear inequalities, exploring what they are, how to solve them, and providing a comprehensive worksheet with answers to help you practice and reinforce your understanding.
What are Systems of Linear Inequalities?
A system of linear inequalities is a set of two or more linear inequalities that share the same variables. These inequalities can be either equalities (e.g., 2x + 3y = 5) or inequalities (e.g., 2x + 3y ≤ 5). The goal of solving a system of linear inequalities is to find the values of the variables that satisfy all the inequalities in the system.
Types of Linear Inequalities
There are two main types of linear inequalities:
- Less than or equal to (≤): This type of inequality is represented by a solid line on the coordinate plane.
- Greater than or equal to (≥): This type of inequality is represented by a dashed line on the coordinate plane.
How to Solve Systems of Linear Inequalities
To solve a system of linear inequalities, you can use the following steps:
- Graph each inequality: Graph each inequality on the coordinate plane, using a solid line for ≤ inequalities and a dashed line for ≥ inequalities.
- Find the intersection: Find the intersection of the lines, which represents the solution to the system.
- Test a point: Test a point in each region to determine which region satisfies all the inequalities.
📝 Note: When graphing inequalities, make sure to test a point in each region to determine which region satisfies the inequality.
Systems of Linear Inequalities Worksheet
Here is a comprehensive worksheet with answers to help you practice and reinforce your understanding of systems of linear inequalities:
Worksheet:
- Solve the system of linear inequalities:
2x + 3y ≤ 6 x - 2y ≥ -3
Solution:
To solve this system, we can graph each inequality on the coordinate plane.
| x | y | 2x + 3y ≤ 6 | x - 2y ≥ -3 |
|---|---|---|---|
| 0 | 0 | 0 ≤ 6 (True) | 0 ≥ -3 (True) |
| 1 | 0 | 2 ≤ 6 (True) | 1 ≥ -3 (True) |
| 0 | 1 | 3 ≤ 6 (True) | -2 ≥ -3 (False) |
From the table, we can see that the solution to the system is the region where x ≥ 0 and y ≤ 2.
Answer: x ≥ 0 and y ≤ 2
- Solve the system of linear inequalities:
x + 2y ≥ 4 3x - 2y ≤ 5
Solution:
To solve this system, we can graph each inequality on the coordinate plane.
| x | y | x + 2y ≥ 4 | 3x - 2y ≤ 5 |
|---|---|---|---|
| 0 | 0 | 0 ≥ 4 (False) | 0 ≤ 5 (True) |
| 1 | 0 | 1 ≥ 4 (False) | 3 ≤ 5 (True) |
| 0 | 1 | 2 ≥ 4 (False) | -2 ≤ 5 (True) |
From the table, we can see that the solution to the system is the region where x ≤ 2 and y ≥ 1.
Answer: x ≤ 2 and y ≥ 1
- Solve the system of linear inequalities:
2x - 3y ≤ 2 x + 4y ≥ 8
Solution:
To solve this system, we can graph each inequality on the coordinate plane.
| x | y | 2x - 3y ≤ 2 | x + 4y ≥ 8 |
|---|---|---|---|
| 0 | 0 | 0 ≤ 2 (True) | 0 ≥ 8 (False) |
| 1 | 0 | 2 ≤ 2 (True) | 1 ≥ 8 (False) |
| 0 | 1 | -3 ≤ 2 (True) | 4 ≥ 8 (False) |
From the table, we can see that the solution to the system is the region where x ≥ 3 and y ≤ 1.
Answer: x ≥ 3 and y ≤ 1
Conclusion
In this blog post, we explored the concept of systems of linear inequalities, including the different types of inequalities and how to solve them. We also provided a comprehensive worksheet with answers to help you practice and reinforce your understanding. Remember to graph each inequality on the coordinate plane and test a point in each region to determine which region satisfies all the inequalities. With practice and patience, you will become proficient in solving systems of linear inequalities.
What is a system of linear inequalities?
+
A system of linear inequalities is a set of two or more linear inequalities that share the same variables.
How do you solve a system of linear inequalities?
+
To solve a system of linear inequalities, you can graph each inequality on the coordinate plane and find the intersection of the lines. Then, test a point in each region to determine which region satisfies all the inequalities.
What are the different types of linear inequalities?
+
There are two main types of linear inequalities: less than or equal to (≤) and greater than or equal to (≥).