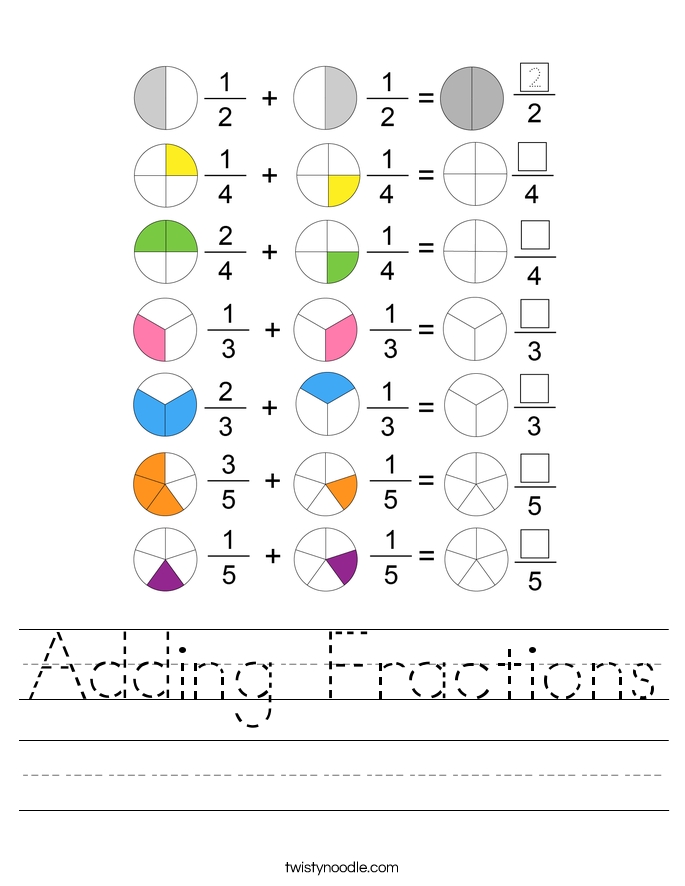
Addition of Fractions Worksheet for Easy Practice

Understanding Fractions: A Comprehensive Guide
Fractions are a fundamental concept in mathematics, and mastering them is crucial for success in various mathematical operations. In this guide, we will delve into the world of fractions, exploring their definition, types, and practical applications. We will also provide a comprehensive worksheet to help you practice and reinforce your understanding of fractions.
What are Fractions?
A fraction is a way to represent a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into.
Types of Fractions
There are several types of fractions, including:
- Proper Fractions: A proper fraction is a fraction where the numerator is less than the denominator. For example, 3⁄4 is a proper fraction.
- Improper Fractions: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 5⁄3 is an improper fraction.
- Mixed Fractions: A mixed fraction is a combination of a whole number and a proper fraction. For example, 2 3⁄4 is a mixed fraction.
Adding and Subtracting Fractions
To add or subtract fractions, we need to have the same denominator. If the denominators are different, we need to find the least common multiple (LCM) of the two denominators.
Step-by-Step Guide to Adding and Subtracting Fractions:
- Check if the denominators are the same. If not, find the LCM of the two denominators.
- Convert both fractions to have the same denominator.
- Add or subtract the numerators.
- Simplify the resulting fraction, if possible.
📝 Note: When adding or subtracting fractions, make sure to keep the denominators the same. If the denominators are different, find the LCM and convert both fractions accordingly.
Multiplying and Dividing Fractions
To multiply fractions, we multiply the numerators and denominators separately. To divide fractions, we invert the second fraction (i.e., flip the numerator and denominator) and then multiply.
Step-by-Step Guide to Multiplying and Dividing Fractions:
- Multiply the numerators and denominators separately to multiply fractions.
- Invert the second fraction and multiply to divide fractions.
📝 Note: When multiplying or dividing fractions, make sure to follow the correct order of operations. Multiply the numerators and denominators separately, and invert the second fraction when dividing.
Real-World Applications of Fractions
Fractions have numerous real-world applications, including:
- Cooking: Fractions are used in recipes to measure ingredients.
- Music: Fractions are used in music to represent time signatures and rhythms.
- Science: Fractions are used in science to represent proportions and ratios.
Fractions Worksheet
Practice your understanding of fractions with this comprehensive worksheet:
| Operation | Fraction 1 | Fraction 2 | Result |
|---|---|---|---|
| Addition | 1/2 | 1/4 | _______ |
| Subtraction | 3/4 | 1/4 | _______ |
| Multiplication | 2/3 | 3/4 | _______ |
| Division | 4/5 | 2/3 | _______ |
Answers:
- Addition: 3⁄4
- Subtraction: 2⁄4
- Multiplication: 6⁄12
- Division: 6⁄10
In conclusion, fractions are a fundamental concept in mathematics, and mastering them is essential for success in various mathematical operations. With this comprehensive guide and worksheet, you can practice and reinforce your understanding of fractions, paving the way for future mathematical success.
What is a fraction?
+A fraction is a way to represent a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number).
How do I add fractions?
+To add fractions, we need to have the same denominator. If the denominators are different, we need to find the least common multiple (LCM) of the two denominators.
How do I multiply fractions?
+To multiply fractions, we multiply the numerators and denominators separately.