Adding Rational Expressions Made Easy with This Worksheet

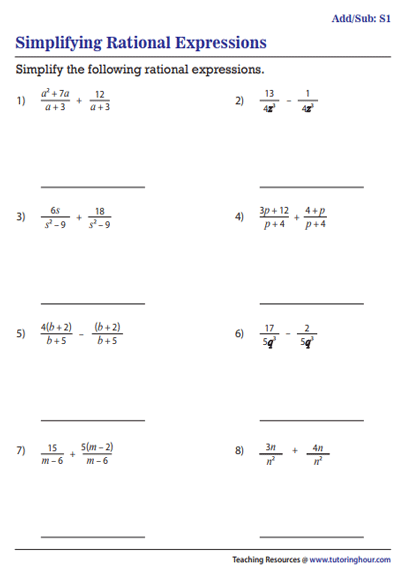
Adding Rational Expressions: A Step-by-Step Guide

Adding rational expressions can be a daunting task for many students. However, with the right approach and practice, it can become a manageable and even enjoyable process. In this article, we will break down the steps to add rational expressions and provide a worksheet to help you practice and reinforce your understanding.

What are Rational Expressions?

Rational expressions are fractions that contain polynomials in both the numerator and denominator. They are used to represent relationships between variables and are commonly encountered in algebra and calculus.

Why is Adding Rational Expressions Important?

Adding rational expressions is an important skill to master because it allows us to combine and simplify complex expressions. This skill is essential in solving equations and inequalities, as well as in graphing functions.

Step-by-Step Guide to Adding Rational Expressions

Adding rational expressions involves several steps:

Step 1: Factor the Denominators

To add rational expressions, we need to factor the denominators. Factoring involves expressing the denominator as a product of its prime factors.

📝 Note: Make sure to factor the denominators completely to ensure that we have a common denominator.

Step 2: Find the Least Common Denominator (LCD)

The least common denominator (LCD) is the smallest multiple that is divisible by both denominators. To find the LCD, we need to identify the highest power of each prime factor that appears in either denominator.

Step 3: Rewrite Each Expression with the LCD

Once we have found the LCD, we need to rewrite each expression with the LCD as the new denominator. This involves multiplying the numerator and denominator of each expression by the necessary factors.

Step 4: Add the Numerators

With the expressions rewritten with the LCD, we can now add the numerators. This involves combining like terms and simplifying the resulting expression.

Step 5: Simplify the Result

Finally, we need to simplify the resulting expression by canceling out any common factors between the numerator and denominator.

Example: Adding Rational Expressions

Let’s consider the following example:

Add: 1/x + 2/(x+1)

To add these expressions, we need to follow the steps outlined above:

• Factor the denominators: x and x+1 are already factored.
• Find the LCD: The LCD is x(x+1).
• Rewrite each expression with the LCD: (x+1)/x(x+1) + 2x/x(x+1)
• Add the numerators: (x+1) + 2x = 3x + 1
• Simplify the result: (3x + 1)/x(x+1)

Worksheet: Adding Rational Expressions

Now that we have covered the steps to add rational expressions, it’s time to practice! Here is a worksheet to help you reinforce your understanding:

Common Mistakes to Avoid

When adding rational expressions, there are several common mistakes to avoid:

• Forgetting to factor the denominators
• Failing to find the LCD
• Not rewriting each expression with the LCD
• Not simplifying the result

By avoiding these common mistakes, you can ensure that you are adding rational expressions correctly.

In summary, adding rational expressions involves several steps: factoring the denominators, finding the LCD, rewriting each expression with the LCD, adding the numerators, and simplifying the result. With practice and reinforcement, you can master this skill and become proficient in adding rational expressions.

The key takeaways from this article are:

• Factor the denominators completely
• Find the LCD and rewrite each expression with the LCD
• Add the numerators and simplify the result
• Avoid common mistakes such as forgetting to factor the denominators or failing to find the LCD

By following these steps and practicing with the worksheet, you can become confident in your ability to add rational expressions.