Mastering Fractions and Mixed Numbers Made Easy

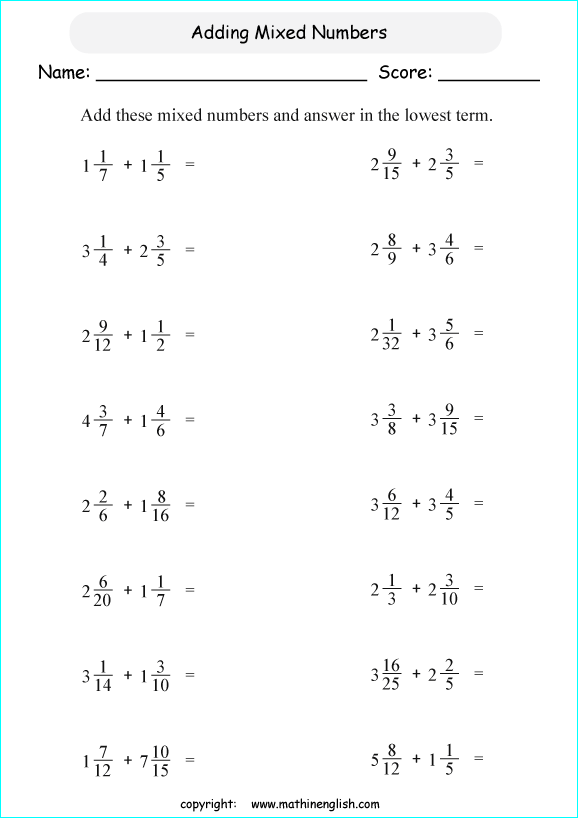
Understanding Fractions and Mixed Numbers

Fractions and mixed numbers are fundamental concepts in mathematics, and mastering them is crucial for success in various mathematical operations. A fraction is a way to represent a part of a whole, while a mixed number is a combination of a whole number and a fraction. In this article, we will explore the world of fractions and mixed numbers, making it easy for you to understand and work with them.

What is a Fraction?

A fraction is a mathematical expression that represents a part of a whole. It consists of two parts: the numerator and the denominator. The numerator is the top number, and it tells us how many equal parts we have. The denominator is the bottom number, and it tells us how many parts the whole is divided into.

For example, in the fraction ³⁄₄, the numerator is 3, and the denominator is 4. This means we have 3 equal parts out of a total of 4 parts.

Types of Fractions

There are several types of fractions, including:

• Proper Fractions: These are fractions where the numerator is less than the denominator. Examples include ¹⁄₂, ²⁄₃, and ³⁄₄.
• Improper Fractions: These are fractions where the numerator is greater than or equal to the denominator. Examples include ³⁄₂, ⁵⁄₄, and ⁷⁄₆.
• Mixed Numbers: These are combinations of a whole number and a proper fraction. Examples include 2 ¹⁄₂, 3 ³⁄₄, and 1 ¹⁄₆.

Working with Fractions

Now that we understand what fractions are, let’s explore how to work with them. Here are some essential operations:

• Adding Fractions: To add fractions, we need to have the same denominator. If the denominators are different, we need to find the least common multiple (LCM) of the two denominators.
• Subtracting Fractions: To subtract fractions, we need to have the same denominator. If the denominators are different, we need to find the LCM of the two denominators.
• Multiplying Fractions: To multiply fractions, we multiply the numerators and multiply the denominators.
• Dividing Fractions: To divide fractions, we invert the second fraction (i.e., flip the numerator and denominator) and then multiply.

Example Problems

Here are some example problems to help you practice working with fractions:

• Add ¹⁄₄ + ¹⁄₄ =?
• Subtract ²⁄₃ - ¹⁄₃ =?
• Multiply ²⁄₃ × ³⁄₄ =?
• Divide ³⁄₄ ÷ ²⁄₃ =?

Mixed Numbers

Mixed numbers are combinations of a whole number and a proper fraction. To work with mixed numbers, we need to follow these steps:

• Converting Mixed Numbers to Improper Fractions: To convert a mixed number to an improper fraction, we multiply the whole number by the denominator and add the numerator.
• Converting Improper Fractions to Mixed Numbers: To convert an improper fraction to a mixed number, we divide the numerator by the denominator and write the remainder as a fraction.

Example Problems

Here are some example problems to help you practice working with mixed numbers:

• Convert 2 ¹⁄₂ to an improper fraction.
• Convert ³⁄₄ to a mixed number.

📝 Note: When working with mixed numbers, it's essential to follow the order of operations (PEMDAS) to ensure accurate results.

Real-World Applications

Fractions and mixed numbers have numerous real-world applications, including:

• Cooking: Recipes often involve fractions and mixed numbers, such as 1 ¹⁄₂ cups of flour or ²⁄₃ cup of sugar.
• Science: Fractions and mixed numbers are used to measure quantities, such as ³⁄₄ cup of water or 2 ¹⁄₂ liters of gas.
• Finance: Fractions and mixed numbers are used to calculate interest rates, discounts, and investments.

Conclusion

Mastering fractions and mixed numbers is crucial for success in mathematics and real-world applications. By understanding the concepts and operations involved, you can confidently work with fractions and mixed numbers. Remember to practice regularly and apply these concepts to real-world scenarios to reinforce your learning.