Negative Numbers Made Easy: Add and Subtract with Confidence

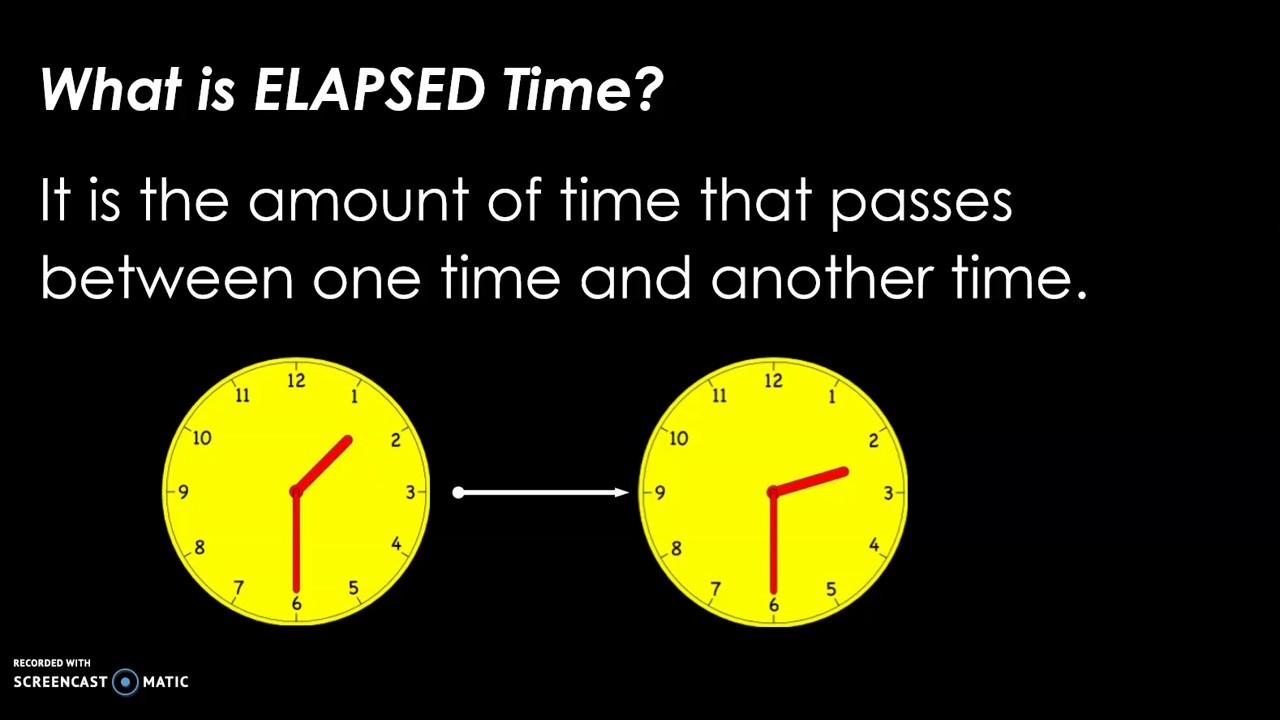
Understanding Negative Numbers
Negative numbers are a fundamental concept in mathematics, and yet, many people struggle to grasp them. In reality, negative numbers are not as daunting as they seem. With a solid understanding of their properties and how to work with them, you’ll become a pro at adding and subtracting negative numbers in no time.
What are Negative Numbers?
Negative numbers are numbers that have a value less than zero. They are represented by a negative sign (-) preceding the number. For example, -3, -5, and -10 are all negative numbers. Negative numbers can be thought of as the opposite of positive numbers. Just as positive numbers represent a quantity that is greater than zero, negative numbers represent a quantity that is less than zero.
The Number Line
One of the best ways to visualize negative numbers is by using a number line. A number line is a straight line with numbers marked at regular intervals. The number line has a zero point in the middle, with positive numbers to the right and negative numbers to the left.
Imagine you’re standing on the zero point of the number line. If you move to the right, you’ll be heading towards positive numbers. If you move to the left, you’ll be heading towards negative numbers.
🤔 Note: The number line is a powerful tool for understanding negative numbers. It can help you visualize how numbers relate to each other and make calculations easier.
Adding Negative Numbers
Adding negative numbers is similar to adding positive numbers, but with a few key differences. When adding negative numbers, you need to follow these rules:
- When adding two negative numbers, add their absolute values (the value without the negative sign) and then apply the negative sign to the result.
- When adding a negative number and a positive number, subtract the absolute value of the negative number from the positive number.
For example:
- -3 + (-5) = -8 (add the absolute values and apply the negative sign)
- -3 + 5 = 2 (subtract the absolute value of the negative number from the positive number)
Subtracting Negative Numbers
Subtracting negative numbers can be a bit tricky, but with the right approach, it’s easy to master. When subtracting negative numbers, follow these rules:
- When subtracting a negative number from a positive number, add the absolute value of the negative number to the positive number.
- When subtracting a negative number from another negative number, subtract the absolute value of the first negative number from the second negative number and then apply the negative sign to the result.
For example:
- 5 - (-3) = 8 (add the absolute value of the negative number to the positive number)
- -5 - (-3) = -2 (subtract the absolute value of the first negative number from the second negative number and apply the negative sign)
Real-World Applications of Negative Numbers
Negative numbers have numerous real-world applications, including:
- Temperature: Negative numbers are used to represent temperatures below zero.
- Finance: Negative numbers are used to represent debts or losses.
- Physics: Negative numbers are used to represent opposite directions or forces.
| Concept | Example |
|---|---|
| Temperature | -5°C (5 degrees below zero) |
| Finance | $-100 (a debt of $100) |
| Physics | -10m/s (a velocity of 10m/s in the opposite direction) |
💡 Note: Negative numbers are used in many real-world applications, making it essential to understand how to work with them.
In conclusion, negative numbers are a fundamental concept in mathematics, and with practice and patience, anyone can become proficient in adding and subtracting them. By understanding the properties of negative numbers and how to work with them, you’ll be able to tackle even the most complex math problems with confidence.
What is a negative number?
+A negative number is a number that has a value less than zero. It is represented by a negative sign (-) preceding the number.
How do I add negative numbers?
+When adding two negative numbers, add their absolute values (the value without the negative sign) and then apply the negative sign to the result. When adding a negative number and a positive number, subtract the absolute value of the negative number from the positive number.
What are some real-world applications of negative numbers?
+Negative numbers have numerous real-world applications, including temperature, finance, and physics.