5 Ways to Master Adding Fractions with 10 and 100
Understanding Fractions
Fractions are a way to represent part of a whole. They consist of two numbers: the numerator and the denominator. The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into. To master adding fractions, we need to understand the concept of equivalent ratios and how to find a common denominator.
Step 1: Understanding Equivalent Ratios
Equivalent ratios are fractions that have the same value, but different numbers. For example, 1⁄2 and 2⁄4 are equivalent ratios because they both represent the same part of the whole. To find equivalent ratios, we can multiply or divide both the numerator and the denominator by the same number.
🤔 Note: When multiplying or dividing both the numerator and the denominator, the value of the fraction remains the same.
Step 2: Finding a Common Denominator
To add fractions, we need to have the same denominator. If the denominators are different, we need to find the least common multiple (LCM) of the two denominators. The LCM is the smallest number that both denominators can divide into evenly.
Example: Finding the LCM of 10 and 100
To find the LCM of 10 and 100, we can list the multiples of each number:
Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 Multiples of 100: 100, 200, 300, 400, 500
The first number that appears in both lists is 100, so the LCM of 10 and 100 is 100.
Step 3: Converting Fractions to Have a Common Denominator
Once we have found the LCM, we can convert both fractions to have the same denominator.
Example: Converting Fractions to Have a Common Denominator
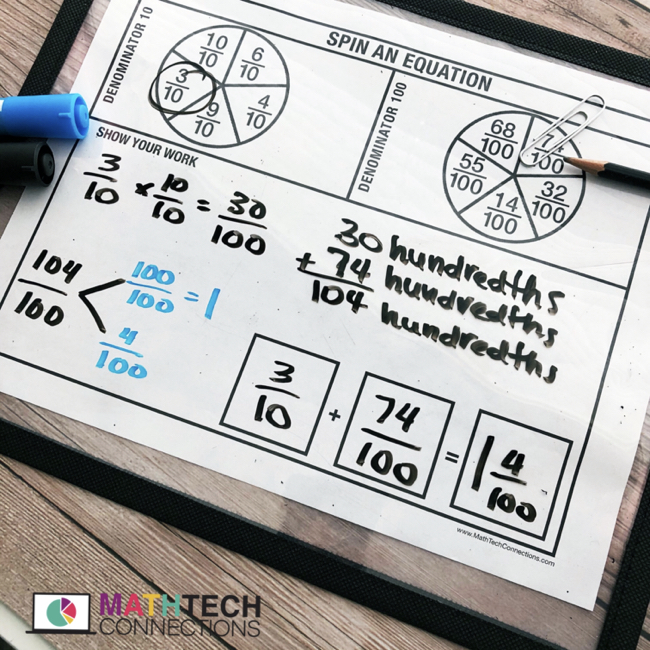
Suppose we want to add 1⁄10 and 3⁄100. To do this, we need to convert both fractions to have a denominator of 100.
1⁄10 = 10⁄100 (multiply numerator and denominator by 10) 3⁄100 = 3⁄100 (no change needed)
Now we can add the fractions:
10⁄100 + 3⁄100 = 13⁄100
Step 4: Adding Fractions with the Same Denominator
Now that we have the same denominator, we can add the fractions by adding the numerators.
Example: Adding Fractions with the Same Denominator
Suppose we want to add 13⁄100 and 25⁄100.
13⁄100 + 25⁄100 = 38⁄100
Step 5: Simplifying the Answer (Optional)
If the answer is not in simplest form, we can simplify it by dividing both the numerator and the denominator by the greatest common divisor (GCD).
Example: Simplifying the Answer
Suppose we want to simplify 38⁄100.
The GCD of 38 and 100 is 2. To simplify the fraction, we can divide both the numerator and the denominator by 2:
38 ÷ 2 = 19 100 ÷ 2 = 50
So the simplified answer is 19⁄50.
| Fraction | Equivalent Ratio | Common Denominator | Answer |
|---|---|---|---|
| 1/10 + 3/100 | 10/100 + 3/100 | 100 | 13/100 |
| 13/100 + 25/100 | 38/100 | 100 | 38/100 |
| 38/100 | 19/50 | 50 | 19/50 |
In conclusion, mastering adding fractions with 10 and 100 requires understanding equivalent ratios, finding a common denominator, converting fractions, adding fractions with the same denominator, and simplifying the answer. By following these steps, you can become proficient in adding fractions with different denominators.
What is the least common multiple (LCM) of 10 and 100?
+The LCM of 10 and 100 is 100.
How do I convert fractions to have a common denominator?
+To convert fractions to have a common denominator, multiply the numerator and denominator of each fraction by the necessary multiples to achieve the common denominator.
What is the greatest common divisor (GCD) of 38 and 100?
+The GCD of 38 and 100 is 2.