5 Ways to Solve Absolute Value Equations

Understanding Absolute Value Equations

Absolute value equations are a type of equation that contains the absolute value of a variable or an expression. These equations are used to represent situations where the distance or magnitude of a quantity is important, but the direction is not. For example, the absolute value of -5 is 5, because the distance from 0 to -5 on the number line is 5 units.

What is Absolute Value?

The absolute value of a number is its distance from 0 on the number line. It is always non-negative, and it can be thought of as the magnitude or size of the number. The absolute value of a number is denoted by vertical bars around the number, such as |x|.

Types of Absolute Value Equations

There are two types of absolute value equations:

• Simple absolute value equations: These are equations where the absolute value of a variable or an expression is equal to a constant. For example, |x| = 5.
• Compound absolute value equations: These are equations where the absolute value of a variable or an expression is equal to another absolute value. For example, |x| = |2x - 3|.

5 Ways to Solve Absolute Value Equations

Here are 5 ways to solve absolute value equations:

Method 1: Splitting the Equation

One way to solve absolute value equations is to split the equation into two separate equations, one with a positive sign and one with a negative sign.

For example, consider the equation |x| = 5.

We can split this equation into two separate equations:

x = 5 x = -5

These two equations represent the two possible solutions to the original absolute value equation.

📝 Note: When splitting an absolute value equation, make sure to include both the positive and negative solutions.

Method 2: Using the Definition of Absolute Value

Another way to solve absolute value equations is to use the definition of absolute value. According to the definition, |x| = x if x ≥ 0, and |x| = -x if x < 0.

For example, consider the equation |x| = 3.

Using the definition of absolute value, we can rewrite this equation as:

x = 3 if x ≥ 0 -x = 3 if x < 0

Solving these two equations, we get:

x = 3 x = -3

These two solutions represent the two possible solutions to the original absolute value equation.

Method 3: Adding and Subtracting the Same Value

A third way to solve absolute value equations is to add and subtract the same value to both sides of the equation.

For example, consider the equation |x - 2| = 4.

We can add 2 to both sides of the equation, which gives us:

|x - 2 + 2| = 4 + 2 |x| = 6

We can then solve this equation by splitting it into two separate equations:

x = 6 x = -6

These two solutions represent the two possible solutions to the original absolute value equation.

Method 4: Using a Table

A fourth way to solve absolute value equations is to use a table.

For example, consider the equation |x + 1| = 3.

We can create a table with two columns, one for the equation x + 1 = 3 and one for the equation x + 1 = -3.

From the table, we can see that the solutions to the original absolute value equation are x = 2 and x = -4.

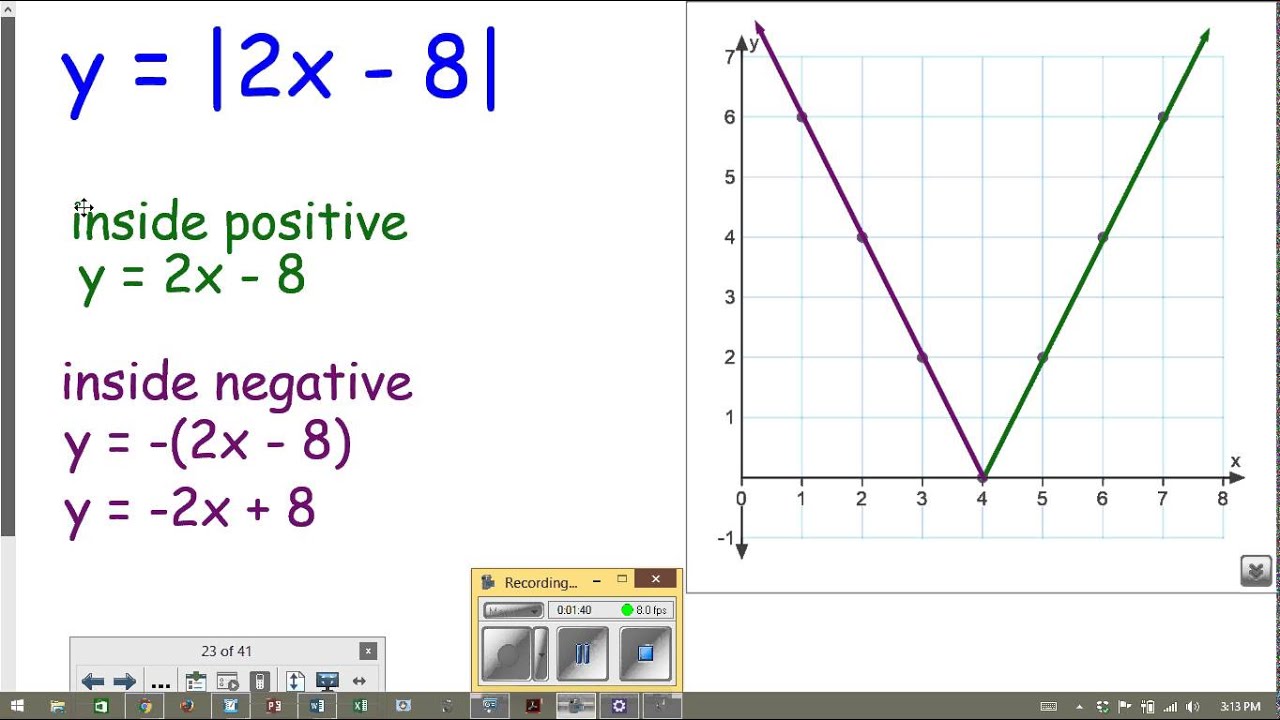
Method 5: Graphing

A fifth way to solve absolute value equations is to graph the equation on a coordinate plane.

For example, consider the equation |x| = 2.

We can graph this equation by plotting the points (2, 0) and (-2, 0) on the coordinate plane.

From the graph, we can see that the solutions to the original absolute value equation are x = 2 and x = -2.

In conclusion, absolute value equations can be solved using a variety of methods, including splitting the equation, using the definition of absolute value, adding and subtracting the same value, using a table, and graphing. Each method has its own strengths and weaknesses, and the choice of method will depend on the specific equation being solved.