5 Ways to Master Parallel Lines and Transversals
Unlocking the Secrets of Parallel Lines and Transversals
Understanding parallel lines and transversals is a crucial aspect of geometry, as it helps students develop problem-solving skills and build a strong foundation in mathematics. However, mastering these concepts can be challenging, especially for those who struggle with visualizing and working with angles. In this article, we’ll explore five effective ways to master parallel lines and transversals, making it easier for students to grasp these essential geometry concepts.
1. Visualize the Concept
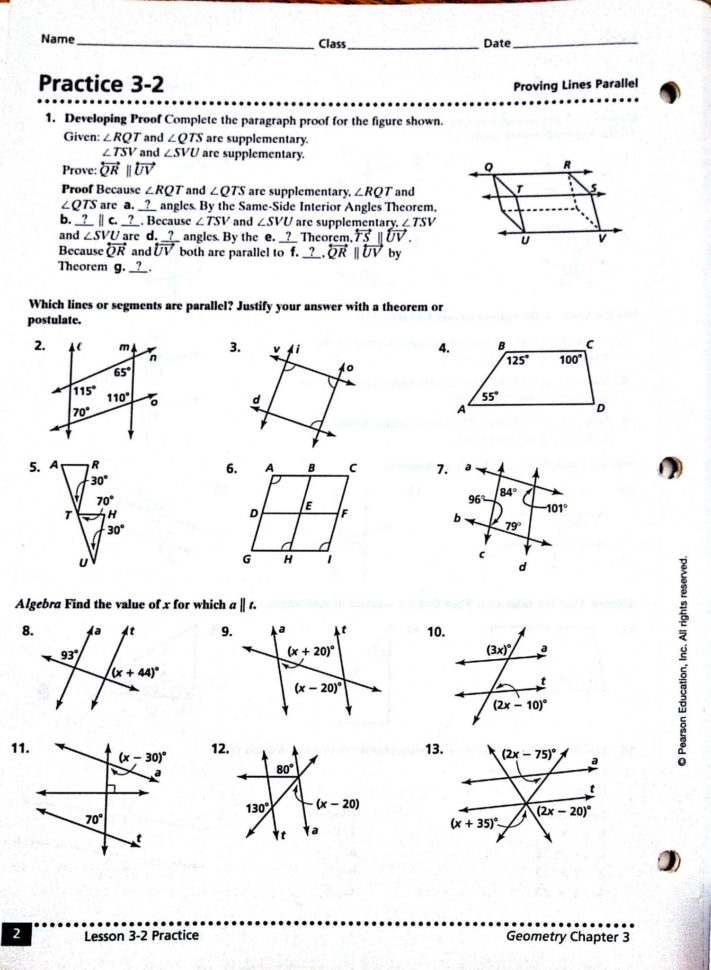
Visualizing parallel lines and transversals is key to understanding how they interact. Start by drawing a diagram with two parallel lines and a transversal line that intersects them. Label the angles formed by the transversal line and the parallel lines. This visual representation will help you see how the angles relate to each other and understand the concepts of corresponding angles, alternate interior angles, and alternate exterior angles.
Types of Angles Formed by Parallel Lines and Transversals
- Corresponding angles: angles that are in the same relative position
- Alternate interior angles: angles that are inside the parallel lines and on opposite sides of the transversal line
- Alternate exterior angles: angles that are outside the parallel lines and on opposite sides of the transversal line
2. Learn the Theorems
There are several theorems related to parallel lines and transversals that you should be familiar with:
- Corresponding Angles Theorem: If two parallel lines are cut by a transversal line, then the corresponding angles are congruent.
- Alternate Interior Angles Theorem: If two parallel lines are cut by a transversal line, then the alternate interior angles are congruent.
- Alternate Exterior Angles Theorem: If two parallel lines are cut by a transversal line, then the alternate exterior angles are congruent.
📝 Note: These theorems can be used to find missing angles in a diagram, making it easier to solve problems involving parallel lines and transversals.
3. Practice with Real-World Examples
Parallel lines and transversals are not just limited to geometry; they can be found in real-world scenarios, such as:
- Railroad tracks: the rails are parallel lines, and the ties are transversals.
- Highway lanes: the lanes are parallel lines, and the lane dividers are transversals.
- Stairs: the steps are parallel lines, and the risers are transversals.
Using real-world examples can help make the concepts more relatable and interesting.
4. Use Online Resources and Games
There are many online resources and games available that can help you practice and master parallel lines and transversals. Some popular options include:
- Khan Academy: offers video lessons and practice exercises on parallel lines and transversals.
- Math Playground: provides interactive games and puzzles that involve parallel lines and transversals.
- GeoGebra: allows you to create and explore interactive geometry diagrams, including those with parallel lines and transversals.
👍 Note: Online resources and games can make learning fun and engaging, but be sure to also practice with traditional worksheets and exercises to reinforce your understanding.
5. Watch Video Tutorials
Video tutorials can be a great way to supplement your learning and get additional help when needed. Some popular YouTube channels for geometry include:
- 3Blue1Brown (Grant Sanderson): offers animated video lessons on geometry and other math topics.
- Crash Course: provides video lessons on geometry and other subjects, hosted by experts in the field.
- Math Antics: offers video lessons and explanations on geometry and other math topics.
📹 Note: Video tutorials can be a great way to review material before a test or to get extra help when you're struggling with a concept.
In conclusion, mastering parallel lines and transversals takes time and practice, but with the right approach, you can become proficient in these essential geometry concepts. By visualizing the concept, learning the theorems, practicing with real-world examples, using online resources and games, and watching video tutorials, you’ll be well on your way to becoming a geometry expert.
What is the difference between corresponding angles and alternate interior angles?
+
Corresponding angles are angles that are in the same relative position, while alternate interior angles are angles that are inside the parallel lines and on opposite sides of the transversal line.
How can I use the theorems to solve problems involving parallel lines and transversals?
+
The theorems can be used to find missing angles in a diagram. For example, if you know that two angles are corresponding angles, you can use the Corresponding Angles Theorem to determine that they are congruent.
What are some real-world examples of parallel lines and transversals?
+
Some real-world examples of parallel lines and transversals include railroad tracks, highway lanes, and stairs.